Bates model engines based on Fourier transform. More...
#include <batesengine.hpp>
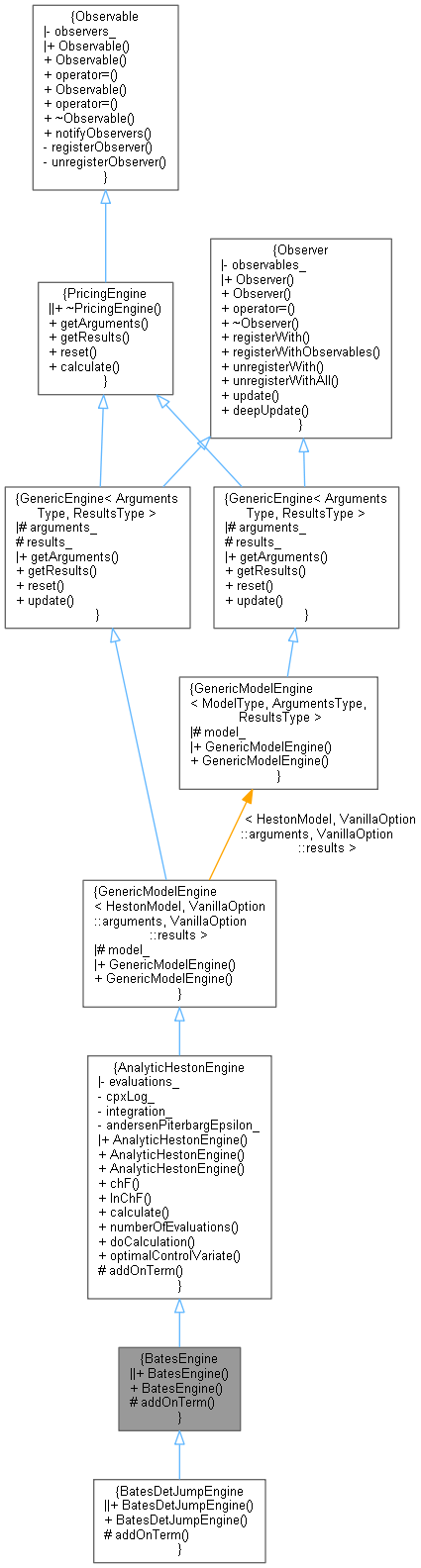
 Inheritance diagram for BatesEngine:
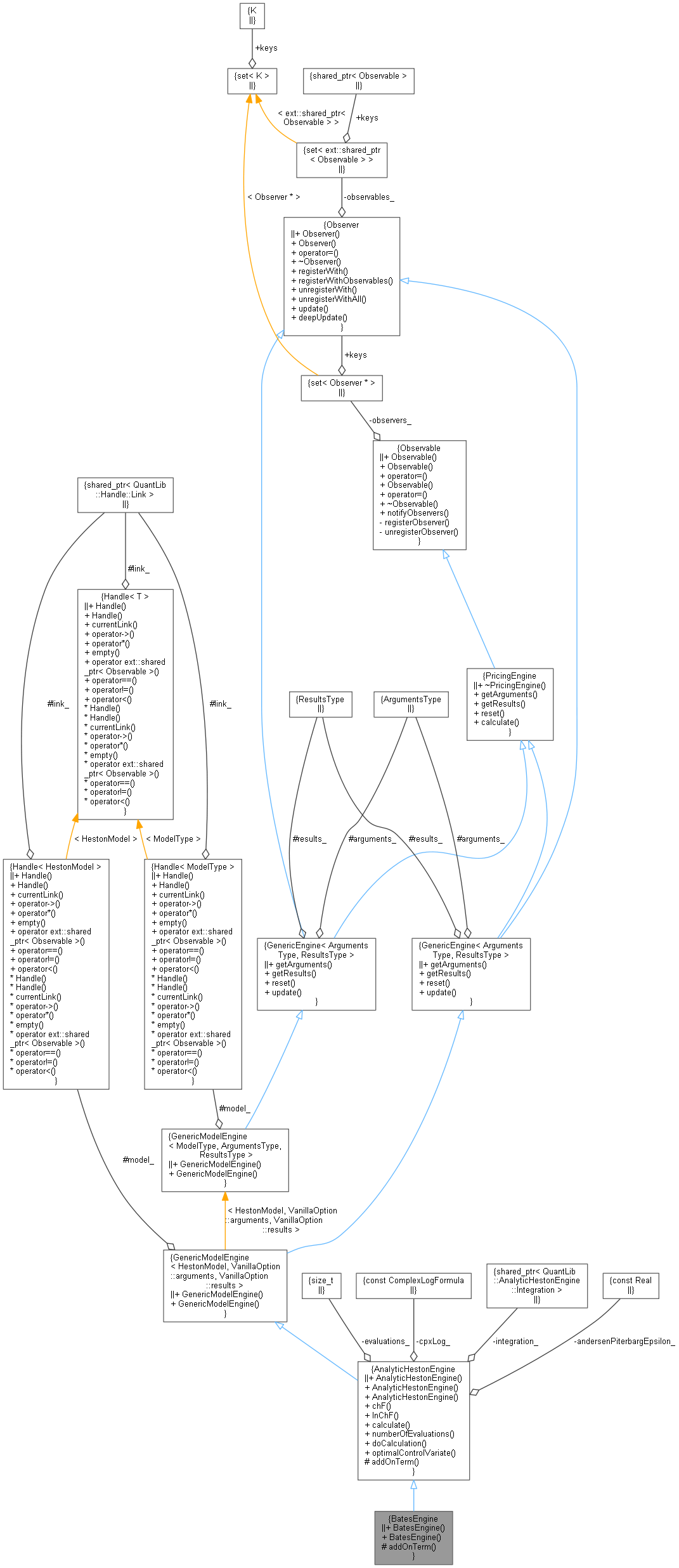
Inheritance diagram for BatesEngine: Collaboration diagram for BatesEngine:
Collaboration diagram for BatesEngine:Public Member Functions | |
| BatesEngine (const ext::shared_ptr< BatesModel > &model, Size integrationOrder=144) | |
| BatesEngine (const ext::shared_ptr< BatesModel > &model, Real relTolerance, Size maxEvaluations) | |
 Public Member Functions inherited from AnalyticHestonEngine Public Member Functions inherited from AnalyticHestonEngine | |
| AnalyticHestonEngine (const ext::shared_ptr< HestonModel > &model, Real relTolerance, Size maxEvaluations) | |
| AnalyticHestonEngine (const ext::shared_ptr< HestonModel > &model, Size integrationOrder=144) | |
| AnalyticHestonEngine (const ext::shared_ptr< HestonModel > &model, ComplexLogFormula cpxLog, const Integration &itg, Real andersenPiterbargEpsilon=1e-25, Real alpha=-0.5) | |
| void | calculate () const override |
| std::complex< Real > | chF (const std::complex< Real > &z, Time t) const |
| std::complex< Real > | lnChF (const std::complex< Real > &z, Time t) const |
| Size | numberOfEvaluations () const |
| Real | priceVanillaPayoff (const ext::shared_ptr< PlainVanillaPayoff > &payoff, const Date &maturity) const |
| Real | priceVanillaPayoff (const ext::shared_ptr< PlainVanillaPayoff > &payoff, Time maturity) const |
 Public Member Functions inherited from GenericModelEngine< HestonModel, VanillaOption::arguments, VanillaOption::results > Public Member Functions inherited from GenericModelEngine< HestonModel, VanillaOption::arguments, VanillaOption::results > | |
| GenericModelEngine (Handle< HestonModel > model=Handle< HestonModel >()) | |
| GenericModelEngine (const ext::shared_ptr< HestonModel > &model) | |
 Public Member Functions inherited from GenericEngine< ArgumentsType, ResultsType > Public Member Functions inherited from GenericEngine< ArgumentsType, ResultsType > | |
| PricingEngine::arguments * | getArguments () const override |
| const PricingEngine::results * | getResults () const override |
| void | reset () override |
| void | update () override |
 Public Member Functions inherited from PricingEngine Public Member Functions inherited from PricingEngine | |
| ~PricingEngine () override=default | |
| virtual arguments * | getArguments () const =0 |
| virtual const results * | getResults () const =0 |
| virtual void | reset ()=0 |
| virtual void | calculate () const =0 |
 Public Member Functions inherited from Observable Public Member Functions inherited from Observable | |
| Observable ()=default | |
| Observable (const Observable &) | |
| Observable & | operator= (const Observable &) |
| Observable (Observable &&)=delete | |
| Observable & | operator= (Observable &&)=delete |
| virtual | ~Observable ()=default |
| void | notifyObservers () |
 Public Member Functions inherited from Observer Public Member Functions inherited from Observer | |
| Observer ()=default | |
| Observer (const Observer &) | |
| Observer & | operator= (const Observer &) |
| virtual | ~Observer () |
| std::pair< iterator, bool > | registerWith (const ext::shared_ptr< Observable > &) |
| void | registerWithObservables (const ext::shared_ptr< Observer > &) |
| Size | unregisterWith (const ext::shared_ptr< Observable > &) |
| void | unregisterWithAll () |
| virtual void | update ()=0 |
| virtual void | deepUpdate () |
Protected Member Functions | |
| std::complex< Real > | addOnTerm (Real phi, Time t, Size j) const override |
| virtual std::complex< Real > | addOnTerm (Real phi, Time t, Size j) const |
Detailed Description
Bates model engines based on Fourier transform.
this classes price european options under the following processes
- Jump-Diffusion with Stochastic Volatility
\[ \begin{array}{rcl} dS(t, S) &=& (r-d-\lambda m) S dt +\sqrt{v} S dW_1 + (e^J - 1) S dN \\ dv(t, S) &=& \kappa (\theta - v) dt + \sigma \sqrt{v} dW_2 \\ dW_1 dW_2 &=& \rho dt \end{array} \]
N is a Poisson process with the intensity \( \lambda \). When a jump occurs the magnitude J has the probability density function \( \omega(J) \).
1.1 Log-Normal Jump Diffusion: BatesEngine
Logarithm of the jump size J is normally distributed
\[ \omega(J) = \frac{1}{\sqrt{2\pi \delta^2}} \exp\left[-\frac{(J-\nu)^2}{2\delta^2}\right] \]
1.2 Double-Exponential Jump Diffusion: BatesDoubleExpEngine
The jump size has an asymmetric double exponential distribution
\[ \begin{array}{rcl} \omega(J)&=& p\frac{1}{\eta_u}e^{-\frac{1}{\eta_u}J} 1_{J>0} + q\frac{1}{\eta_d}e^{\frac{1}{\eta_d}J} 1_{J<0} \\ p + q &=& 1 \end{array} \]
- Stochastic Volatility with Jump Diffusion and Deterministic Jump Intensity
\[ \begin{array}{rcl} dS(t, S) &=& (r-d-\lambda m) S dt +\sqrt{v} S dW_1 + (e^J - 1) S dN \\ dv(t, S) &=& \kappa (\theta - v) dt + \sigma \sqrt{v} dW_2 \\ d\lambda(t) &=& \kappa_\lambda(\theta_\lambda-\lambda) dt \\ dW_1 dW_2 &=& \rho dt \end{array} \]
2.1 Log-Normal Jump Diffusion with Deterministic Jump Intensity BatesDetJumpEngine
2.2 Double-Exponential Jump Diffusion with Deterministic Jump Intensity BatesDoubleExpDetJumpEngine
References:
D. Bates, Jumps and stochastic volatility: exchange rate processes implicit in Deutsche mark options, Review of Financial Sudies 9, 69-107.
A. Sepp, Pricing European-Style Options under Jump Diffusion Processes with Stochastic Volatility: Applications of Fourier Transform (http://math.ut.ee/~spartak/papers/stochjumpvols.pdf)
- Tests:
- the correctness of the returned value is tested by reproducing results available in web/literature, testing against QuantLib's jump diffusion engine and comparison with Black pricing.
Definition at line 106 of file batesengine.hpp.
Constructor & Destructor Documentation
◆ BatesEngine() [1/2]
|
explicit |
Definition at line 26 of file batesengine.cpp.
◆ BatesEngine() [2/2]
| BatesEngine | ( | const ext::shared_ptr< BatesModel > & | model, |
| Real | relTolerance, | ||
| Size | maxEvaluations | ||
| ) |
Definition at line 32 of file batesengine.cpp.
Member Function Documentation
◆ addOnTerm()
Reimplemented from AnalyticHestonEngine.
Reimplemented in BatesDetJumpEngine.
Definition at line 39 of file batesengine.cpp.
 Here is the caller graph for this function:
Here is the caller graph for this function: