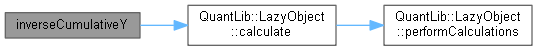Abstract base class for one-factor copula models. More...
#include <onefactorcopula.hpp>
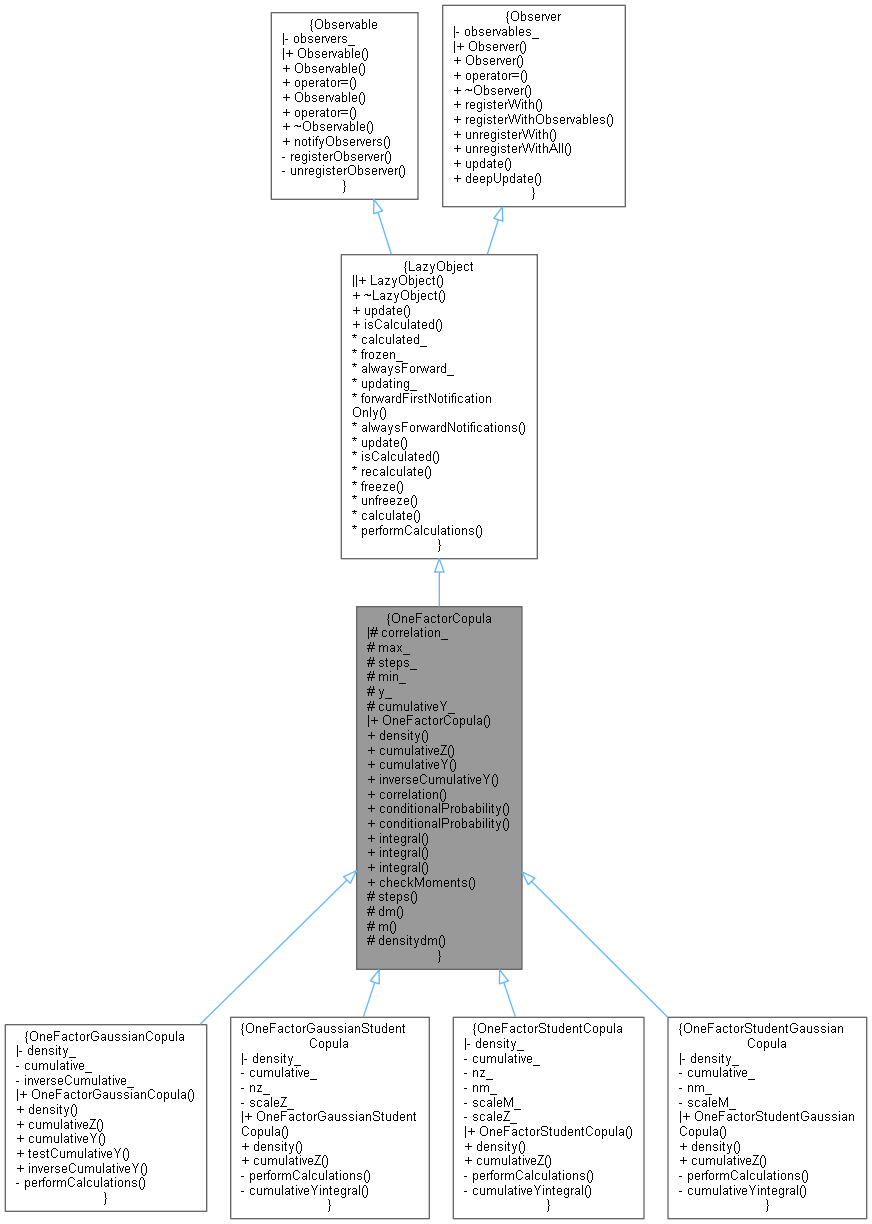
 Inheritance diagram for OneFactorCopula:
Inheritance diagram for OneFactorCopula: Collaboration diagram for OneFactorCopula:
Collaboration diagram for OneFactorCopula:Public Member Functions | |
| OneFactorCopula (Handle< Quote > correlation, Real maximum=5.0, Size integrationSteps=50, Real minimum=-5.0) | |
| virtual Real | density (Real m) const =0 |
| Density function of M. More... | |
| virtual Real | cumulativeZ (Real z) const =0 |
| Cumulative distribution of Z. More... | |
| virtual Real | cumulativeY (Real y) const |
| Cumulative distribution of Y. More... | |
| virtual Real | inverseCumulativeY (Real p) const |
| Inverse cumulative distribution of Y. More... | |
| Real | correlation () const |
| Single correlation parameter. More... | |
| Real | conditionalProbability (Real prob, Real m) const |
| Conditional probability. More... | |
| std::vector< Real > | conditionalProbability (const std::vector< Real > &prob, Real m) const |
| Vector of conditional probabilities. More... | |
| Real | integral (Real p) const |
| template<class F > | |
| Real | integral (const F &f, std::vector< Real > &probabilities) const |
| template<class F > | |
| Distribution | integral (const F &f, const std::vector< Real > &nominals, const std::vector< Real > &probabilities) const |
| int | checkMoments (Real tolerance) const |
 Public Member Functions inherited from LazyObject Public Member Functions inherited from LazyObject | |
| LazyObject () | |
| ~LazyObject () override=default | |
| void | update () override |
| bool | isCalculated () const |
| void | forwardFirstNotificationOnly () |
| void | alwaysForwardNotifications () |
| void | recalculate () |
| void | freeze () |
| void | unfreeze () |
 Public Member Functions inherited from Observable Public Member Functions inherited from Observable | |
| Observable ()=default | |
| Observable (const Observable &) | |
| Observable & | operator= (const Observable &) |
| Observable (Observable &&)=delete | |
| Observable & | operator= (Observable &&)=delete |
| virtual | ~Observable ()=default |
| void | notifyObservers () |
 Public Member Functions inherited from Observer Public Member Functions inherited from Observer | |
| Observer ()=default | |
| Observer (const Observer &) | |
| Observer & | operator= (const Observer &) |
| virtual | ~Observer () |
| std::pair< iterator, bool > | registerWith (const ext::shared_ptr< Observable > &) |
| void | registerWithObservables (const ext::shared_ptr< Observer > &) |
| Size | unregisterWith (const ext::shared_ptr< Observable > &) |
| void | unregisterWithAll () |
| virtual void | update ()=0 |
| virtual void | deepUpdate () |
Protected Member Functions | |
| Size | steps () const |
| Real | dm (Size i) const |
| Real | m (Size i) const |
| Real | densitydm (Size i) const |
 Protected Member Functions inherited from LazyObject Protected Member Functions inherited from LazyObject | |
| virtual void | calculate () const |
| virtual void | performCalculations () const =0 |
Protected Attributes | |
| Handle< Quote > | correlation_ |
| Real | max_ |
| Size | steps_ |
| Real | min_ |
| std::vector< Real > | y_ |
| std::vector< Real > | cumulativeY_ |
 Protected Attributes inherited from LazyObject Protected Attributes inherited from LazyObject | |
| bool | calculated_ = false |
| bool | frozen_ = false |
| bool | alwaysForward_ |
Additional Inherited Members | |
 Public Types inherited from Observer Public Types inherited from Observer | |
| typedef set_type::iterator | iterator |
Detailed Description
Abstract base class for one-factor copula models.
Reference: John Hull and Alan White, The Perfect Copula, June 2006
Let \(Q_i(t)\) be the cumulative probability of default of counterparty i before time t.
In a one-factor model, consider random variables
\[ Y_i = a_i\,M+\sqrt{1-a_i^2}\:Z_i \]
where \(M\) and \(Z_i\) have independent zero-mean unit-variance distributions and \(-1\leq a_i \leq 1\). The correlation between \(Y_i\) and \(Y_j\) is then \(a_i a_j\).
Let \(F_Y(y)\) be the cumulative distribution function of \(Y_i\). \(y\) is mapped to \(t\) such that percentiles match, i.e. \(F_Y(y)=Q_i(t)\) or \(y=F_Y^{-1}(Q_i(t))\).
Now let \(F_Z(z)\) be the cumulated distribution function of \(Z_i\). For given realization of \(M\), this determines the distribution of \(y\):
\[ Prob \,(Y_i < y|M) = F_Z \left( \frac{y-a_i\,M}{\sqrt{1-a_i^2}}\right) \qquad \mbox{or} \qquad Prob \,(t_i < t|M) = F_Z \left( \frac{F_Y^{-1}(Q_i(t))-a_i\,M} {\sqrt{1-a_i^2}} \right) \]
The distribution functions of \( M, Z_i \) are specified in derived classes. The distribution function of \( Y \) is then given by the convolution
\[ F_Y(y) = Prob\,(Y<y) = \int_{-\infty}^\infty\,\int_{-\infty}^{\infty}\: D_Z(z)\,D_M(m) \quad \Theta \left(y - a\,m - \sqrt{1-a^2}\,z\right)\,dm\,dz, \qquad \Theta (x) = \left\{ \begin{array}{ll} 1 & x \geq 0 \\ 0 & x < 0 \end{array}\right. \]
where \( D_Z(z) \) and \( D_M(m) \) are the probability densities of \( Z\) and \( M, \) respectively.
This convolution can also be written
\[ F(y) = Prob \,(Y < y) = \int_{-\infty}^\infty D_M(m)\,dm\: \int_{-\infty}^{g(y,a,m)} D_Z(z)\,dz, \qquad g(y,a,m) = \frac{y - a\cdot m}{\sqrt{1-a^2}}, \qquad a < 1 \]
or
\[ F(y) = Prob \,(Y < y) = \int_{-\infty}^\infty D_Z(z)\,dz\: \int_{-\infty}^{h(y,a,z)} D_M(m)\,dm, \qquad h(y,a,z) = \frac{y - \sqrt{1 - a^2}\cdot z}{a}, \qquad a > 0. \]
In general, \( F_Y(y) \) needs to be computed numerically.
Definition at line 102 of file onefactorcopula.hpp.
Constructor & Destructor Documentation
◆ OneFactorCopula()
Member Function Documentation
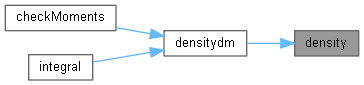
◆ density()
Density function of M.
Derived classes must override this method and ensure zero mean and unit variance.
Implemented in OneFactorGaussianCopula, OneFactorStudentCopula, OneFactorGaussianStudentCopula, and OneFactorStudentGaussianCopula.
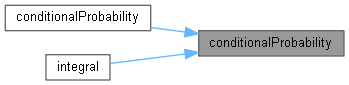
 Here is the caller graph for this function:
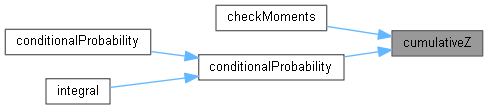
Here is the caller graph for this function:◆ cumulativeZ()
Cumulative distribution of Z.
Derived classes must override this method and ensure zero mean and unit variance.
Implemented in OneFactorGaussianCopula, OneFactorStudentCopula, OneFactorGaussianStudentCopula, and OneFactorStudentGaussianCopula.
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ cumulativeY()
Cumulative distribution of Y.
This is the default implementation based on tabulated data. The table needs to be filled by derived classes. If analytic calculation is feasible, this method can also be overridden.
Reimplemented in OneFactorGaussianCopula.
Definition at line 57 of file onefactorcopula.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ inverseCumulativeY()
Inverse cumulative distribution of Y.
This is the default implementation based on tabulated data. The table needs to be filled by derived classes. If analytic calculation is feasible, this method can also be overridden.
Reimplemented in OneFactorGaussianCopula.
Definition at line 78 of file onefactorcopula.cpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ correlation()
| Real correlation | ( | ) | const |
Single correlation parameter.
Definition at line 263 of file onefactorcopula.hpp.
 Here is the call graph for this function:
Here is the call graph for this function:◆ conditionalProbability() [1/2]
Conditional probability.
\[ \hat p(m) = F_Z \left( \frac{F_Y^{-1}(p)-a\,m}{\sqrt{1-a^2}}\right) \]
Definition at line 27 of file onefactorcopula.cpp.
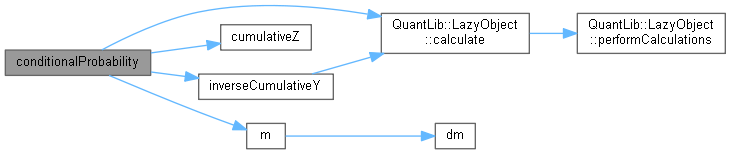
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ conditionalProbability() [2/2]
Vector of conditional probabilities.
\[ \hat p_i(m) = F_Z \left( \frac{F_Y^{-1}(p_i)-a\,m}{\sqrt{1-a^2}} \right) \]
Definition at line 45 of file onefactorcopula.cpp.
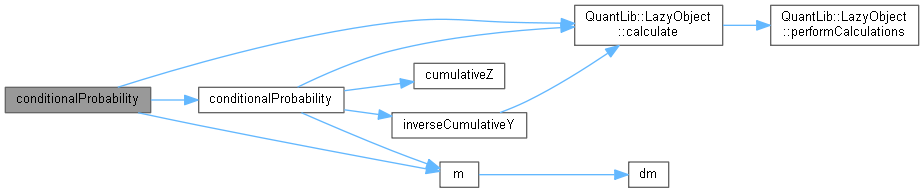
 Here is the call graph for this function:
Here is the call graph for this function:◆ integral() [1/3]
Integral over the density \( \rho(m) \) of M and the conditional probability related to p:
\[ \int_{-\infty}^\infty\,dm\,\rho(m)\, F_Z \left( \frac{F_Y^{-1}(p)-a\,m}{\sqrt{1-a^2}}\right) \]
Definition at line 169 of file onefactorcopula.hpp.
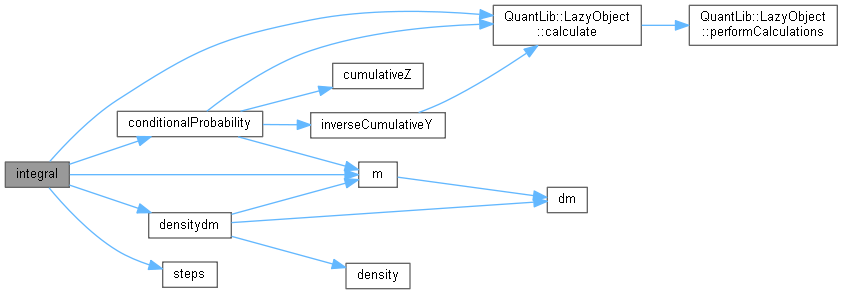
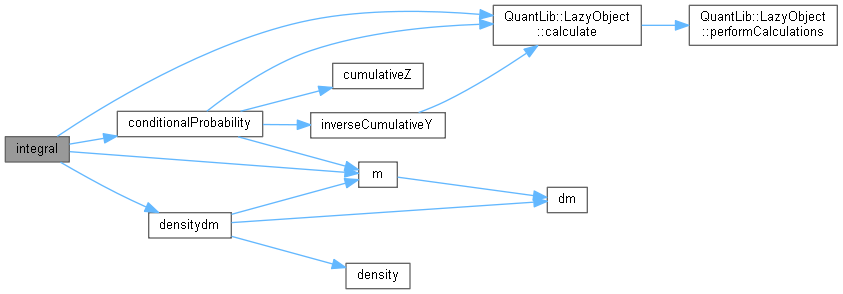
 Here is the call graph for this function:
Here is the call graph for this function:◆ integral() [2/3]
Integral over the density \( \rho(m) \) of M and a one-dimensional function \( f \) of conditional probabilities related to the input vector of probabilities p:
\[ \int_{-\infty}^\infty\,dm\,\rho(m)\, f (\hat p_1, \hat p_2, \dots, \hat p_N), \qquad \hat p_i (m) = F_Z \left( \frac{F_Y^{-1}(p_i)-a\,m}{\sqrt{1-a^2}} \right) \]
Definition at line 194 of file onefactorcopula.hpp.
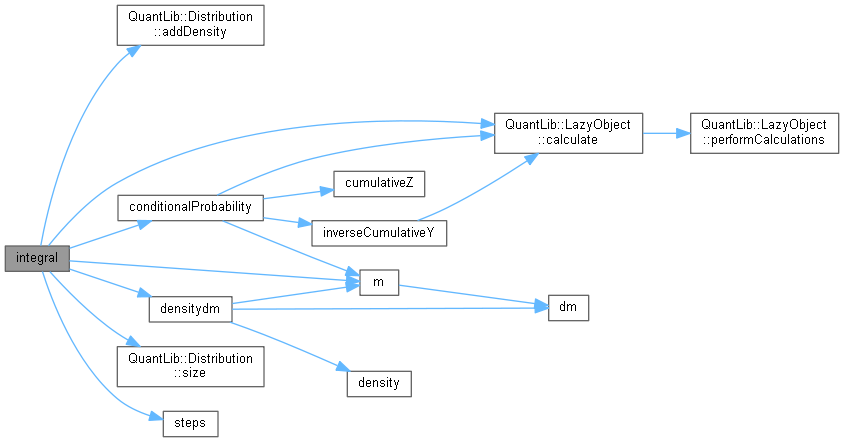
 Here is the call graph for this function:
Here is the call graph for this function:◆ integral() [3/3]
| Distribution integral | ( | const F & | f, |
| const std::vector< Real > & | nominals, | ||
| const std::vector< Real > & | probabilities | ||
| ) | const |
Integral over the density \( \rho(m) \) of M and a multi-dimensional function \( f \) of conditional probabilities related to the input vector of probabilities p:
\[ \int_{-\infty}^\infty\,dm\,\rho(m)\, f (\hat p_1, \hat p_2, \dots, \hat p_N), \qquad \hat p_i = F_Z \left( \frac{F_Y^{-1}(p_i)-a\,m}{\sqrt{1-a^2}}\right) \]
Definition at line 218 of file onefactorcopula.hpp.
 Here is the call graph for this function:
Here is the call graph for this function:◆ checkMoments()
| int checkMoments | ( | Real | tolerance | ) | const |
Check moments (unit norm, zero mean and unit variance) of the distributions of M, Z, and Y by numerically integrating the respective density. Parameter tolerance is the maximum tolerable absolute error.
Definition at line 99 of file onefactorcopula.cpp.
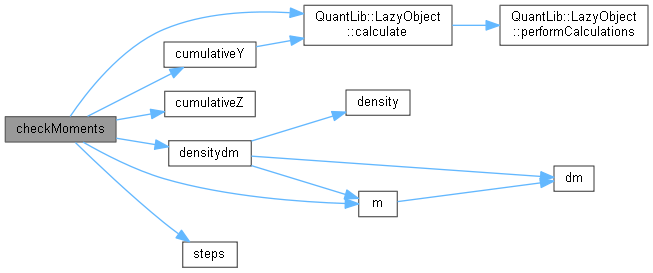
 Here is the call graph for this function:
Here is the call graph for this function:◆ steps()
|
protected |
◆ dm()
◆ m()
Definition at line 276 of file onefactorcopula.hpp.
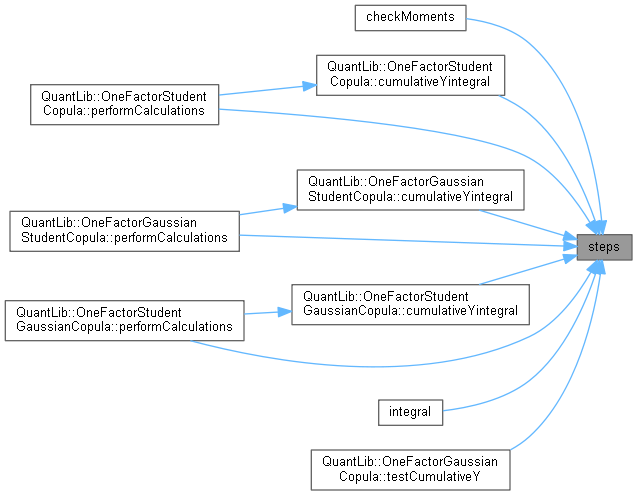
 Here is the call graph for this function:
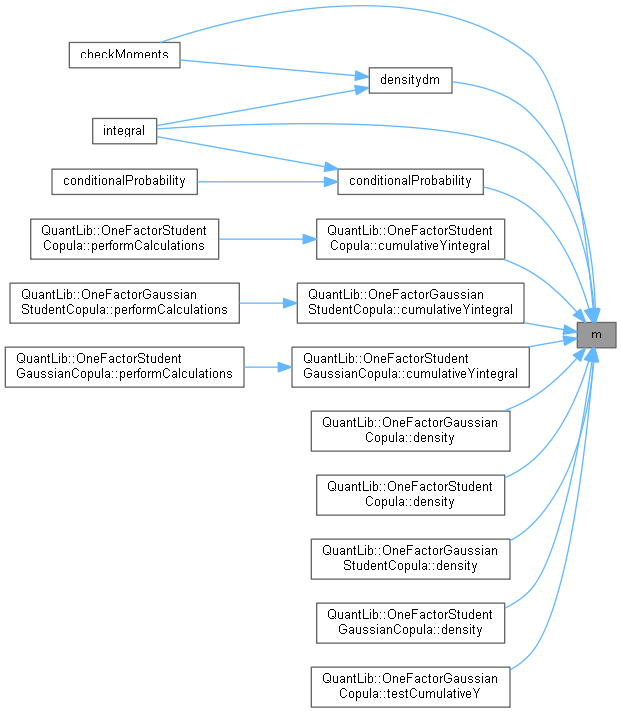
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ densitydm()
Definition at line 281 of file onefactorcopula.hpp.
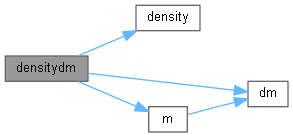
 Here is the call graph for this function:
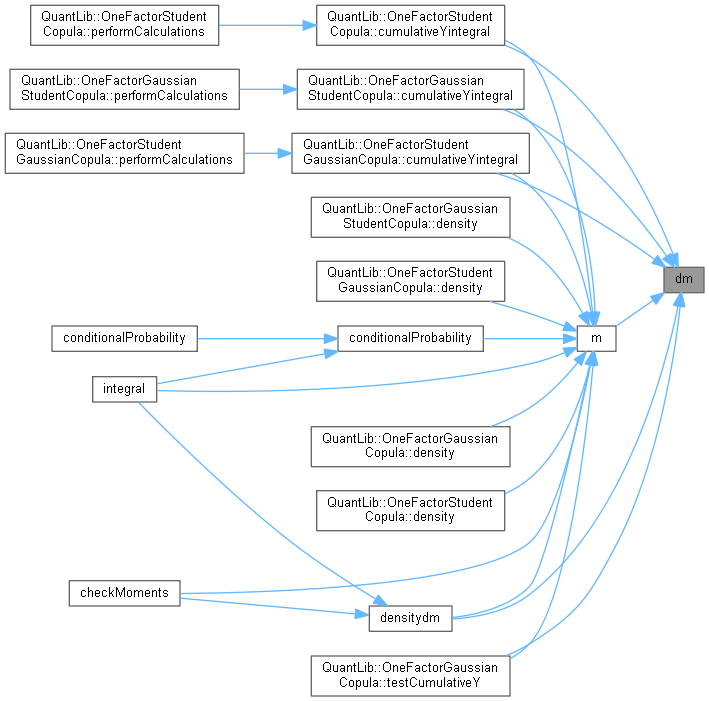
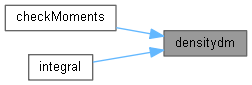
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:Member Data Documentation
◆ correlation_
Definition at line 242 of file onefactorcopula.hpp.
◆ max_
|
mutableprotected |
Definition at line 243 of file onefactorcopula.hpp.
◆ steps_
|
mutableprotected |
Definition at line 244 of file onefactorcopula.hpp.
◆ min_
|
mutableprotected |
Definition at line 245 of file onefactorcopula.hpp.
◆ y_
|
mutableprotected |
Definition at line 248 of file onefactorcopula.hpp.
◆ cumulativeY_
|
mutableprotected |
Definition at line 249 of file onefactorcopula.hpp.