Generic multifactor latent variable model. More...

#include <latentmodel.hpp>

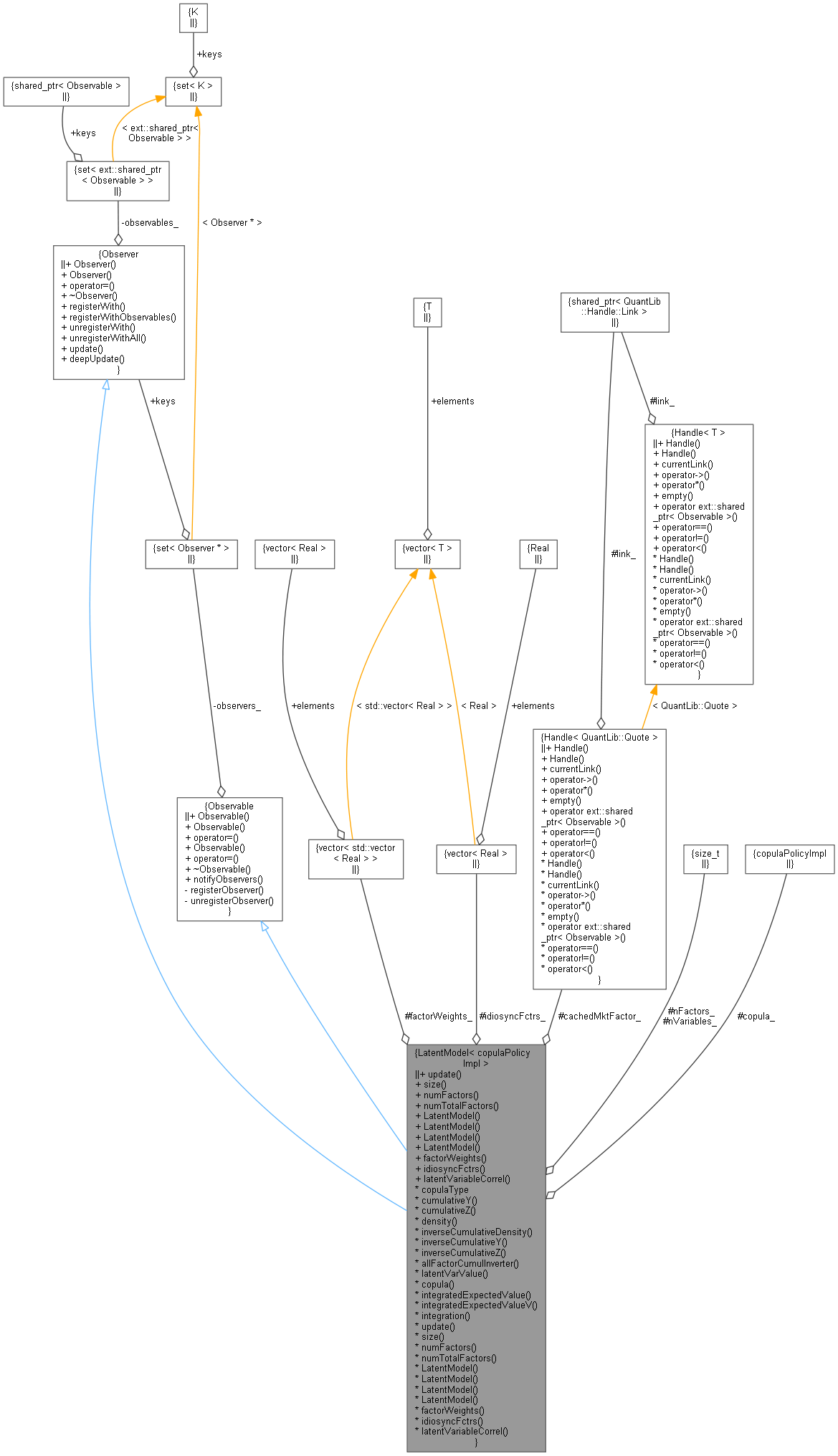
Inheritance diagram for LatentModel< copulaPolicyImpl >:

Collaboration diagram for LatentModel< copulaPolicyImpl >:

Classes
class	FactorSampler

class	IntegrationFactory

Public Member Functions
Latent model direct integration facility.
void	update () override

Latent model random factor number generator facility.
Size	size () const

Size	numFactors () const
	Number of systemic factors. More...

Size	numTotalFactors () const
	Number of total free random factors; systemic and idiosyncratic. More...

	LatentModel (const std::vector< std::vector< Real > > &factorsWeights, const typename copulaType::initTraits &ini=typename copulaType::initTraits())

	LatentModel (const std::vector< Real > &factorsWeight, const typename copulaType::initTraits &ini=typename copulaType::initTraits())

	LatentModel (Real correlSqr, Size nVariables, const typename copulaType::initTraits &ini=typename copulaType::initTraits())

	LatentModel (const Handle< Quote > &singleFactorCorrel, Size nVariables, const typename copulaType::initTraits &ini=typename copulaType::initTraits())

const std::vector< std::vector< Real > > &	factorWeights () const
	Provides values of the factors \( a_{i,k} \). More...

const std::vector< Real > &	idiosyncFctrs () const
	Provides values of the normalized idiosyncratic factors \( Z_i \). More...

Real	latentVariableCorrel (Size iVar1, Size iVar2) const
	Latent variable correlations: More...

Public Member Functions inherited from Observer
	Observer ()=default

	Observer (const Observer &)

Observer &	operator= (const Observer &)

virtual	~Observer ()

std::pair< iterator, bool >	registerWith (const ext::shared_ptr< Observable > &)

void	registerWithObservables (const ext::shared_ptr< Observer > &)

Size	unregisterWith (const ext::shared_ptr< Observable > &)

void	unregisterWithAll ()

virtual void	update ()=0

virtual void	deepUpdate ()

Public Member Functions inherited from Observable
	Observable ()

	Observable (const Observable &)

Observable &	operator= (const Observable &)

	Observable (Observable &&)=delete

Observable &	operator= (Observable &&)=delete

virtual	~Observable ()=default

void	notifyObservers ()

Copula interface.
typedef copulaPolicyImpl	copulaType

Probability	cumulativeY (Real val, Size iVariable) const

Probability	cumulativeZ (Real z) const
	Cumulative distribution of Z, the idiosyncratic/error factors. More...

Probability	density (const std::vector< Real > &m) const
	Density function of M, the market/systemic factors. More...

Real	inverseCumulativeDensity (Probability p, Size iFactor) const
	Inverse cumulative distribution of the systemic factor iFactor. More...

Real	inverseCumulativeY (Probability p, Size iVariable) const

Real	inverseCumulativeZ (Probability p) const

std::vector< Real >	allFactorCumulInverter (const std::vector< Real > &probs) const

Real	latentVarValue (const std::vector< Real > &allFactors, Size iVar) const

const copulaType &	copula () const

Integration facility interface
std::vector< std::vector< Real > >	factorWeights_

Handle< Quote >	cachedMktFactor_

std::vector< Real >	idiosyncFctrs_

Size	nFactors_
	Number of systemic factors. More...

Size	nVariables_
	Number of latent model variables, idiosyncratic terms or model dim. More...

copulaType	copula_

Real	integratedExpectedValue (const ext::function< Real(const std::vector< Real > &v1)> &f) const

std::vector< Real >	integratedExpectedValueV (const ext::function< std::vector< Real >(const std::vector< Real > &v1)> &f) const

virtual const ext::shared_ptr< LMIntegration > &	integration () const

Additional Inherited Members
Public Types inherited from Observer
typedef set_type::iterator	iterator

Detailed Description

template<class copulaPolicyImpl>
class QuantLib::LatentModel< copulaPolicyImpl >

Generic multifactor latent variable model.

: In this model set up one considers latent (random) variables \( Y_i \) described by:
\[ \begin{array}{ccccc} Y_1 & = & \sum_k M_k a_{1,k} & + \sqrt{1-\sum_k a_{1,k}^2} Z_1 & \sim \Phi_{Y_1}\nonumber \\ ... & = & ... & ... & \nonumber \\ Y_i & = & \sum_k M_k a_{i,k} & + \sqrt{1-\sum_k a_{i,k}^2} Z_i & \sim \Phi_{Y_i}\nonumber \\ ... & = & ... & ... & \nonumber \\ Y_N & = & \sum_k M_k a_{N,k} & + \sqrt{1-\sum_k a_{N,k}^2} Z_N & \sim \Phi_{Y_N} \end{array} \]
where the systemic \( M_k \) and idiosyncratic \( Z_i \) (this last one known as error term in some contexts) random variables have independent zero-mean unit-variance distributions. A restriction of the model implemented here is that the N idiosyncratic variables all follow the same probability law \( \Phi_Z(z)\) (but they are still independent random variables) Also the model is normalized so that: \(-1\leq a_{i,k} \leq 1\) (technically the \(Y_i\) are convex linear combinations). The correlation between \(Y_i\) and \(Y_j\) is then \(\sum_k a_{i,k} a_{j,k}\). \(\Phi_{Y_i}\) denotes the cumulative distribution function of \(Y_i\) which in general differs for each latent variable.

: In its single factor set up this model is usually employed in derivative pricing and it is best to use it through integration of the desired statistical properties of the model; in its multifactorial version (with typically around a dozen factors) it is used in the context of portfolio risk metrics; because of the number of variables it is best to opt for a simulation to compute model properties/magnitudes. For this reason this class template provides a random factor sample interface and an integration interface that will be instantiated by derived concrete models as needed. The class is neutral on the integration and random generation algorithms

The latent variables are typically treated as unobservable magnitudes and they serve to model one or several magnitudes related to them through some function

\[ \begin{array}{ccc} F_i(Y_i) & = & F_i(\sum_k M_k a_{i,k} + \sqrt{1-\sum_k a_{i,k}^2} Z_i )\nonumber \\ & = & F_i(M_1,..., M_k, ..., M_K, Z_i) \end{array} \]

The transfer function can have a more generic form: \(F_i(Y_1,....,Y_N)\) but here the model is restricted to a one to one relation between the latent variables and the modelled ones. Also it is assumed that \(F_i(y_i; \tau)\) is monotonic in \(y_i\); it can then be inverted and the relation of the cumulative probability of \(F_i\) and \(Y_i\) is simple:

\[ \int_{\infty}^b \phi_{F_i} df = \int_{\infty}^{F_i^{-1}(b)} \phi_{Y_i} dy \]

If \(t\) is some value of the functional or modelled variable, \(y\) is mapped to \(t\) such that percentiles match, i.e. \(F_Y(y)=Q_i(t)\) or \(y=F_Y^{-1}(Q_i(t))\). The class provides an integration facility of arbitrary functions dependent on the model states. It also provides random number generation interfaces for usage of the model in monte carlo simulations.

Now let \(\Phi_Z(z)\) be the cumulated distribution function of (all equal as mentioned) \(Z_i\). For a given realization of \(M_k\), this determines the distribution of \(y\):

\[ Prob \,(Y_i < y|M_k) = \Phi_Z \left( \frac{y-\sum_k a_{i,k}\,M_k} {\sqrt{1-\sum_k a_{i,k}^2}}\right) \qquad \mbox{or} \qquad Prob \,(t_i < t|M) = \Phi_Z \left( \frac {F_{Y_{i}}^{-1}(Q_i(t))-\sum_k a_{i,k}\,M_k} {\sqrt{1-\sum_k a_{i,k}^2}} \right) \]

The distribution functions of \( M_k, Z_i \) are specified in specific copula template classes. The distribution function of \( Y_i \) is then given by the convolution

\[ F_{Y_{i}}(y) = Prob\,(Y_i<y) = \int_{-\infty}^\infty\,\cdots\,\int_{-\infty}^{\infty}\: D_Z(z)\,\prod_k D_{M_{k}}(m_k) \quad \Theta \left(y - \sum_k a_{i,k}m_k - \sqrt{1-\sum_k a_{i,k}^2}\,z\right)\,d\bar{m}\,dz, \qquad \Theta (x) = \left\{ \begin{array}{ll} 1 & x \geq 0 \\ 0 & x < 0 \end{array}\right. \]

where \( D_Z(z) \) and \( D_M(m) \) are the probability densities of \( Z\) and \( M, \) respectively.

: This convolution can also be written
\[ F_{Y_{i}}(y) = Prob \,(Y_i < y) = \int_{-\infty}^\infty\,\cdots\,\int_{-\infty}^{\infty} D_{M_{k}}(m_k)\,dm_k\: \int_{-\infty}^{g(y,\vec{a},\vec{m})} D_Z(z)\,dz, \qquad g(y,\vec{a},\vec{m}) = \frac{y - \sum_k a_{i,k}m_k} {\sqrt{1-\sum_k a_{i,k}^2}}, \qquad \sum_k a_{i,k}^2 < 1 \]
In general, \( F_{Y_{i}}(y) \) needs to be computed numerically.

: The policy class template separates the copula function (the distributions involved) and the functionality (i.e. what the latent
model represents: a default probability, a recovery...). Since the
copula methods for the probabilities are to be called repeatedly from an integration or a MC simulation, virtual tables are avoided and template parameter mechnics is preferred.

: There is nothing at this level enforncing the requirement on the factor distributions to be of zero mean and unit variance. Thats the user responsibility and the model fails to behave correctly if it is not the case.

: Derived classes should implement a modelled magnitude (default time, etc) and will provide probability distributions and conditional values. They could also provide functionality for the parameter inversion problem, the (e.g.) time at which the modeled variable first takes a given value. This problem has solution/sense depending on the transfer function \(F_i(Y_i)\) characteristics.

To make direct integration and simulation time efficient virtual functions have been avoided in accessing methods in the copula policy and in the sampling of the random factors

Definition at line 278 of file latentmodel.hpp.

Member Typedef Documentation

◆ copulaType

typedef copulaPolicyImpl copulaType

Definition at line 285 of file latentmodel.hpp.

Constructor & Destructor Documentation

◆ LatentModel() [1/4]

LatentModel	(	const std::vector< std::vector< Real > > &	factorsWeights,
		const typename copulaType::initTraits &	ini = `typename copulaType::initTraits()`
	)

explicit

Constructs a LM with an arbitrary number of latent variables and factors given by the dimensions of the passed matrix.

Parameters

factorsWeights	Ordering is factorWeights_[iVar][iFactor]
ini	Initialization variables. Trait type from the copula policy to allow for static policies (this solution needs to be revised, possibly drop the static policy and create a policy member in LatentModel)

◆ LatentModel() [2/4]

LatentModel	(	const std::vector< Real > &	factorsWeight,
		const typename copulaType::initTraits &	ini = `typename copulaType::initTraits()`
	)

explicit

Constructs a LM with an arbitrary number of latent variables depending only on one random factor but contributing to each latent variable through different weights.

Parameters

factorsWeight	Ordering is factorWeights_[iVariable]
ini	Initialization variables. Trait type from the copula policy to allow for static policies (this solution needs to be revised, possibly drop the static policy and create a policy member in LatentModel)

◆ LatentModel() [3/4]

LatentModel	(	Real	correlSqr,
		Size	nVariables,
		const typename copulaType::initTraits &	ini = `typename copulaType::initTraits()`
	)

explicit

Constructs a LM with an arbitrary number of latent variables depending only on one random factor with the same weight for all latent variables.

correlSqr is the weight, same for all.

ini is a trait type from the copula policy, to allow for static policies (this solution needs to be revised, possibly drop the static policy and create a policy member in LatentModel)

◆ LatentModel() [4/4]

LatentModel	(	const Handle< Quote > &	singleFactorCorrel,
		Size	nVariables,
		const typename copulaType::initTraits &	ini = `typename copulaType::initTraits()`
	)

explicit

Constructs a LM with an arbitrary number of latent variables depending only on one random factor with the same weight for all latent variables. The weight is observed and this constructor is intended to be used when the model relates to a market value.

singleFactorCorrel is the weight/mkt-factor, same for all.

ini is a trait type from the copula policy, to allow for static policies (this solution needs to be revised, possibly drop the static policy and create a policy member in LatentModel)

Member Function Documentation

◆ update()

void update ( )

overridevirtual

This method must be implemented in derived classes. An instance of Observer does not call this method directly: instead, it will be called by the observables the instance registered with when they need to notify any changes.

Implements Observer.

Definition at line 710 of file latentmodel.hpp.

Here is the caller graph for this function:

◆ cumulativeY()

Probability cumulativeY	(	Real	val,
		Size	iVariable
	)		const

Cumulative probability of the \( Y_i \) modelled latent random variable to take a given value.

Definition at line 289 of file latentmodel.hpp.

◆ cumulativeZ()

Probability cumulativeZ ( Real z ) const

Cumulative distribution of Z, the idiosyncratic/error factors.

Definition at line 293 of file latentmodel.hpp.

◆ density()

Probability density ( const std::vector< Real > & m ) const

Density function of M, the market/systemic factors.

Definition at line 297 of file latentmodel.hpp.

◆ inverseCumulativeDensity()

Real inverseCumulativeDensity	(	Probability	p,
		Size	iFactor
	)		const

Inverse cumulative distribution of the systemic factor iFactor.

Definition at line 305 of file latentmodel.hpp.

◆ inverseCumulativeY()

Real inverseCumulativeY	(	Probability	p,
		Size	iVariable
	)		const

Inverse cumulative value of the i-th random latent variable with a given probability.

Definition at line 310 of file latentmodel.hpp.

◆ inverseCumulativeZ()

Real inverseCumulativeZ ( Probability p ) const

Inverse cumulative value of the idiosyncratic variable with a given probability.

Definition at line 315 of file latentmodel.hpp.

◆ allFactorCumulInverter()

std::vector< Real > allFactorCumulInverter ( const std::vector< Real > & probs ) const

All factor cumulative inversion. Used in integrations and sampling. Inverts all the cumulative random factors probabilities in the model. These are all the systemic factors plus all the idiosyncratic ones, so the size of the inversion is the number of systemic factors plus the number of latent modelled variables

Definition at line 323 of file latentmodel.hpp.

◆ latentVarValue()

Real latentVarValue	(	const std::vector< Real > &	allFactors,
		Size	iVar
	)		const

The value of the latent variable Y_i conditional to (given) a set of values of the factors.

The passed allFactors vector contains values for all the independent factors in the model (systemic and idiosyncratic, in that order). A full sample is required, i.e. all the idiosyncratic values are expected to be present even if only the relevant one is used.

Definition at line 337 of file latentmodel.hpp.

Here is the call graph for this function:

◆ copula()

const copulaType & copula ( ) const

Definition at line 348 of file latentmodel.hpp.

◆ size()

Size size ( ) const

Definition at line 498 of file latentmodel.hpp.

◆ numFactors()

Size numFactors ( ) const

Number of systemic factors.

Definition at line 500 of file latentmodel.hpp.

Here is the caller graph for this function:

◆ numTotalFactors()

Size numTotalFactors ( ) const

Number of total free random factors; systemic and idiosyncratic.

Definition at line 502 of file latentmodel.hpp.

◆ factorWeights()

const std::vector< std::vector< Real > > & factorWeights ( ) const

Provides values of the factors \( a_{i,k} \).

Definition at line 560 of file latentmodel.hpp.

◆ idiosyncFctrs()

const std::vector< Real > & idiosyncFctrs ( ) const

Provides values of the normalized idiosyncratic factors \( Z_i \).

Definition at line 564 of file latentmodel.hpp.

◆ latentVariableCorrel()

Real latentVariableCorrel	(	Size	iVar1,
		Size	iVar2
	)		const

Latent variable correlations:

Definition at line 567 of file latentmodel.hpp.

◆ integratedExpectedValue()

Real integratedExpectedValue ( const ext::function< Real(const std::vector< Real > &v1)> & f ) const

Integrates an arbitrary scalar function over the density domain(i.e. computes its expected value).

Definition at line 580 of file latentmodel.hpp.

Here is the call graph for this function:

◆ integratedExpectedValueV()

std::vector< Real > integratedExpectedValueV ( const ext::function< std::vector< Real >(const std::vector< Real > &v1)> & f ) const

Integrates an arbitrary vector function over the density domain(i.e. computes its expected value).

Definition at line 590 of file latentmodel.hpp.

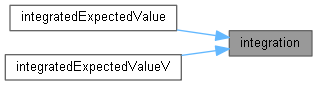
Here is the call graph for this function:

◆ integration()

virtual const ext::shared_ptr< LMIntegration > & integration ( ) const

protectedvirtual

Reimplemented in DefaultLatentModel< copulaPolicy >, and SpotRecoveryLatentModel< copulaPolicy >.

Definition at line 602 of file latentmodel.hpp.

Here is the caller graph for this function:

Member Data Documentation

◆ factorWeights_

std::vector<std::vector<Real> > factorWeights_

mutableprotected

Definition at line 608 of file latentmodel.hpp.

◆ cachedMktFactor_

Handle<Quote> cachedMktFactor_

mutableprotected

Definition at line 622 of file latentmodel.hpp.

◆ idiosyncFctrs_

std::vector<Real> idiosyncFctrs_

mutableprotected

Definition at line 627 of file latentmodel.hpp.

◆ nFactors_

Size nFactors_

mutableprotected

Number of systemic factors.

Definition at line 629 of file latentmodel.hpp.

◆ nVariables_

Size nVariables_

mutableprotected

Number of latent model variables, idiosyncratic terms or model dim.

Definition at line 631 of file latentmodel.hpp.

◆ copula_

copulaType copula_

mutableprotected

Definition at line 633 of file latentmodel.hpp.

Classes

Public Member Functions

Copula interface.

Integration facility interface

Additional Inherited Members

Detailed Description

Member Typedef Documentation

◆ copulaType

Constructor & Destructor Documentation

◆ LatentModel() [1/4]

◆ LatentModel() [2/4]

◆ LatentModel() [3/4]

◆ LatentModel() [4/4]

Member Function Documentation

◆ update()

◆ cumulativeY()

◆ cumulativeZ()

◆ density()

◆ inverseCumulativeDensity()

◆ inverseCumulativeY()

◆ inverseCumulativeZ()

◆ allFactorCumulInverter()

◆ latentVarValue()

◆ copula()

◆ size()

◆ numFactors()

◆ numTotalFactors()

◆ factorWeights()

◆ idiosyncFctrs()

◆ latentVariableCorrel()

◆ integratedExpectedValue()

◆ integratedExpectedValueV()

◆ integration()

Member Data Documentation

◆ factorWeights_

◆ cachedMktFactor_

◆ idiosyncFctrs_

◆ nFactors_

◆ nVariables_

◆ copula_