Integral of a 1-dimensional function using the Gauss quadratures method. More...
#include <gaussianquadratures.hpp>
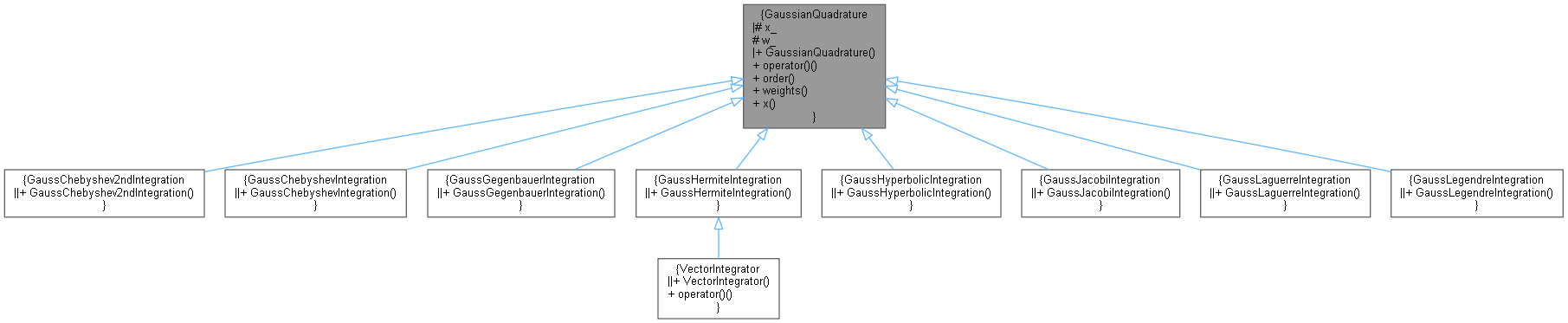
 Inheritance diagram for GaussianQuadrature:
Inheritance diagram for GaussianQuadrature: Collaboration diagram for GaussianQuadrature:
Collaboration diagram for GaussianQuadrature:Public Member Functions | |
| GaussianQuadrature (Size n, const GaussianOrthogonalPolynomial &p) | |
| template<class F > | |
| Real | operator() (const F &f) const |
| Size | order () const |
| const Array & | weights () |
| const Array & | x () |
Protected Attributes | |
| Array | x_ |
| Array | w_ |
Detailed Description
Integral of a 1-dimensional function using the Gauss quadratures method.
References: Gauss quadratures and orthogonal polynomials
G.H. Gloub and J.H. Welsch: Calculation of Gauss quadrature rule. Math. Comput. 23 (1986), 221-230
"Numerical Recipes in C", 2nd edition, Press, Teukolsky, Vetterling, Flannery,
- Tests:
- the correctness of the result is tested by checking it against known good values.
Definition at line 48 of file gaussianquadratures.hpp.
Constructor & Destructor Documentation
◆ GaussianQuadrature()
| GaussianQuadrature | ( | Size | n, |
| const GaussianOrthogonalPolynomial & | p | ||
| ) |
Member Function Documentation
◆ operator()()
◆ order()
| Size order | ( | ) | const |
Definition at line 71 of file gaussianquadratures.hpp.
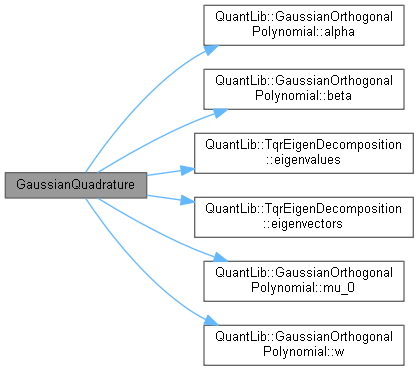
 Here is the call graph for this function:
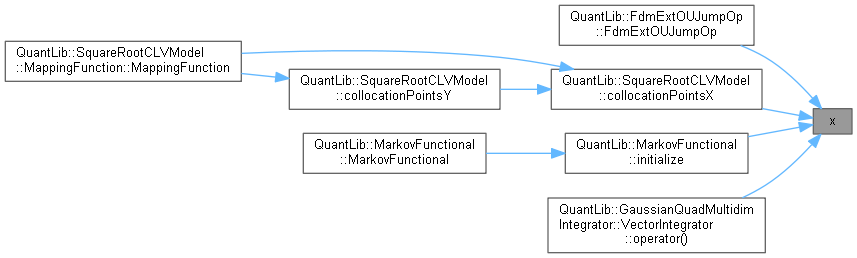
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ weights()
| const Array & weights | ( | ) |
◆ x()
| const Array & x | ( | ) |
Member Data Documentation
◆ x_
|
protected |
Definition at line 76 of file gaussianquadratures.hpp.
◆ w_
|
protected |
Definition at line 76 of file gaussianquadratures.hpp.