GaussianOrthogonalPolynomial Class Reference

orthogonal polynomial for Gaussian quadratures More...

#include <gaussianorthogonalpolynomial.hpp>

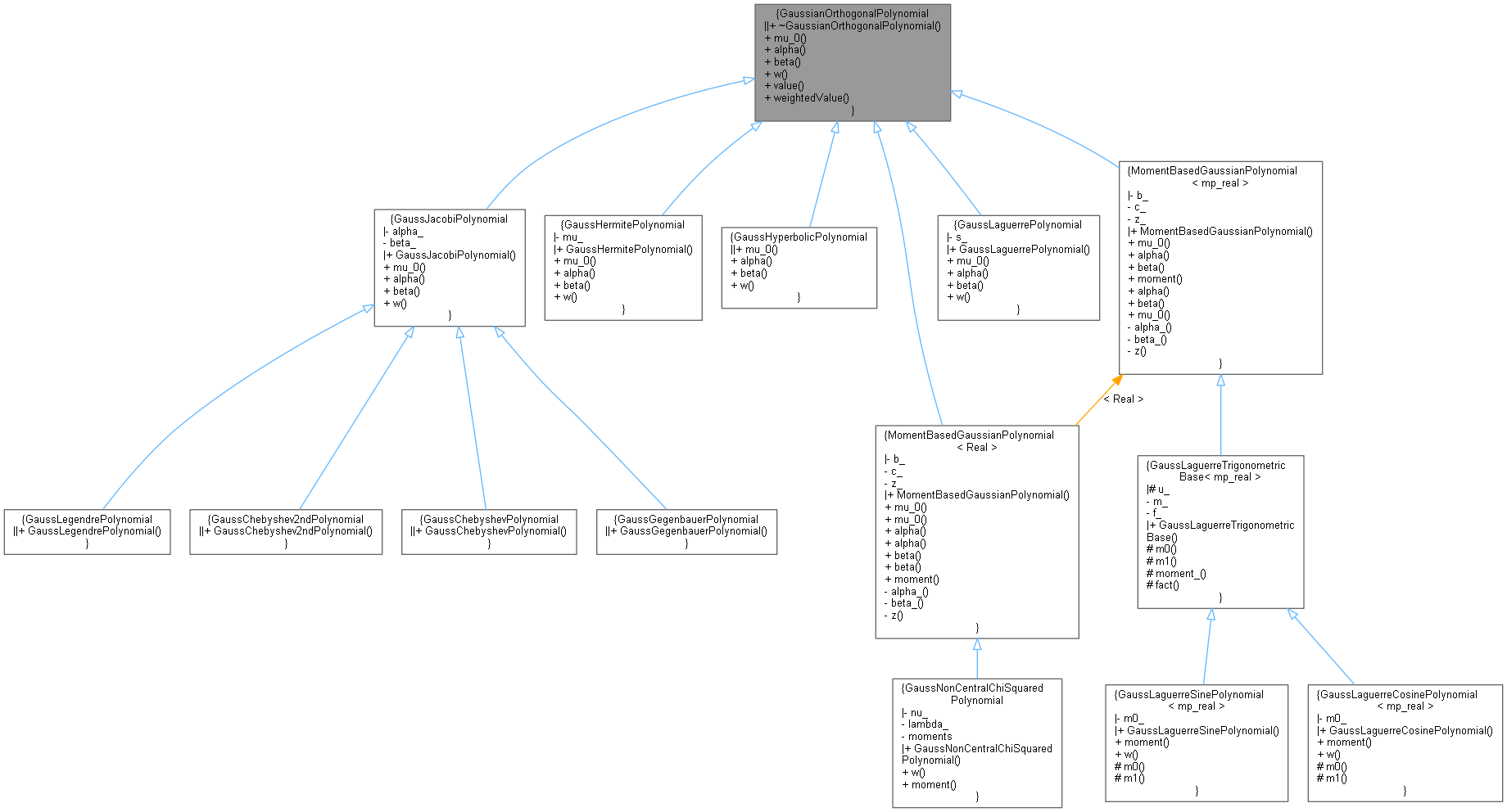
Inheritance diagram for GaussianOrthogonalPolynomial:

Collaboration diagram for GaussianOrthogonalPolynomial:

Public Member Functions
virtual	~GaussianOrthogonalPolynomial ()=default
virtual Real	mu_0 () const =0
virtual Real	alpha (Size i) const =0
virtual Real	beta (Size i) const =0
virtual Real	w (Real x) const =0
Real	value (Size i, Real x) const
Real	weightedValue (Size i, Real x) const

Detailed Description

orthogonal polynomial for Gaussian quadratures

References: Gauss quadratures and orthogonal polynomials

G.H. Gloub and J.H. Welsch: Calculation of Gauss quadrature rule. Math. Comput. 23 (1986), 221-230

"Numerical Recipes in C", 2nd edition, Press, Teukolsky, Vetterling, Flannery,

The polynomials are defined by the three-term recurrence relation

\[ P_{k+1}(x)=(x-\alpha_k) P_k(x) - \beta_k P_{k-1}(x) \]

and

\[ \mu_0 = \int{w(x)dx} \]

Definition at line 50 of file gaussianorthogonalpolynomial.hpp.

Constructor & Destructor Documentation

~GaussianOrthogonalPolynomial()

virtual ~GaussianOrthogonalPolynomial ( )

virtualdefault

Member Function Documentation

mu_0()

virtual Real mu_0 ( ) const

pure virtual

Implemented in MomentBasedGaussianPolynomial< mp_real >, MomentBasedGaussianPolynomial< Real >, GaussLaguerrePolynomial, GaussHermitePolynomial, GaussJacobiPolynomial, GaussHyperbolicPolynomial, MomentBasedGaussianPolynomial< mp_real >, and MomentBasedGaussianPolynomial< Real >.

Here is the caller graph for this function:

alpha()

virtual Real alpha ( Size  i ) const

pure virtual

Implemented in GaussLaguerrePolynomial, GaussHermitePolynomial, GaussJacobiPolynomial, GaussHyperbolicPolynomial, MomentBasedGaussianPolynomial< mp_real >, MomentBasedGaussianPolynomial< Real >, MomentBasedGaussianPolynomial< mp_real >, and MomentBasedGaussianPolynomial< Real >.

Here is the caller graph for this function:

beta()

virtual Real beta ( Size  i ) const

pure virtual

Implemented in GaussLaguerrePolynomial, GaussHermitePolynomial, GaussJacobiPolynomial, GaussHyperbolicPolynomial, MomentBasedGaussianPolynomial< mp_real >, MomentBasedGaussianPolynomial< Real >, MomentBasedGaussianPolynomial< mp_real >, and MomentBasedGaussianPolynomial< Real >.

Here is the caller graph for this function:

w()

virtual Real w ( Real  x ) const

pure virtual

Implemented in GaussNonCentralChiSquaredPolynomial, GaussLaguerrePolynomial, GaussHermitePolynomial, GaussJacobiPolynomial, GaussHyperbolicPolynomial, GaussLaguerreCosinePolynomial< mp_real >, and GaussLaguerreSinePolynomial< mp_real >.

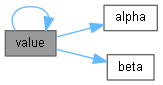
Here is the caller graph for this function:

value()

Real value	(	Size	i,
		Real	x
	)		const

Definition at line 32 of file gaussianorthogonalpolynomial.cpp.

Here is the call graph for this function:

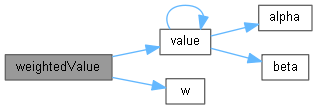
Here is the caller graph for this function:

weightedValue()

Real weightedValue	(	Size	i,
		Real	x
	)		const

Definition at line 44 of file gaussianorthogonalpolynomial.cpp.

Here is the call graph for this function:

Here is the caller graph for this function: