#include <momentbasedgaussianpolynomial.hpp>
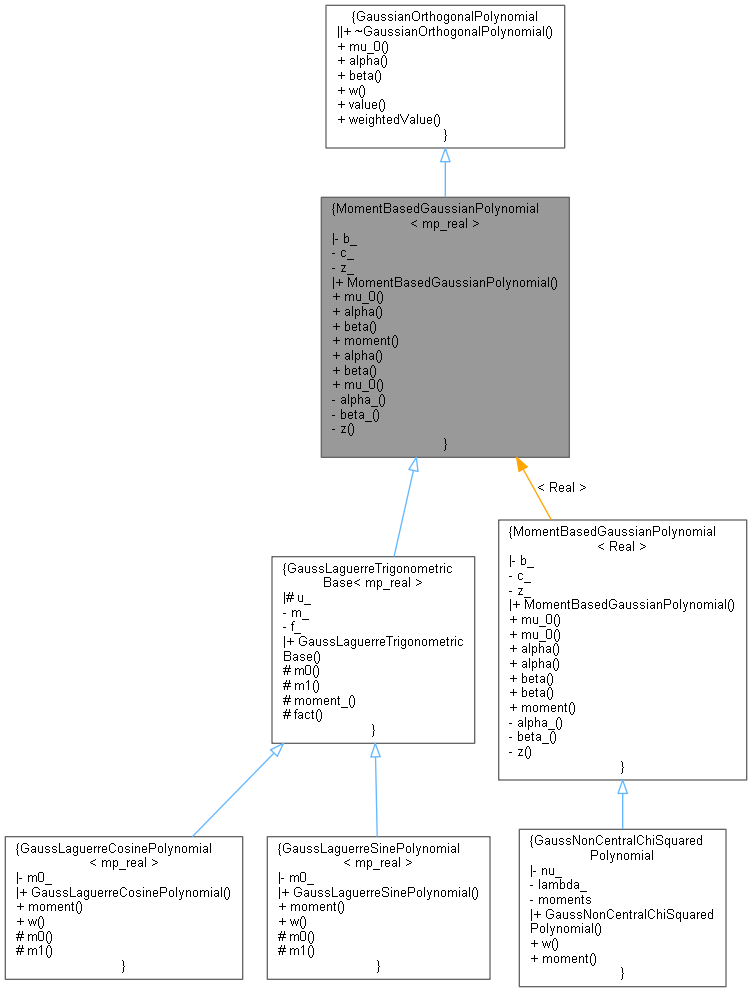
 Inheritance diagram for MomentBasedGaussianPolynomial< mp_real >:
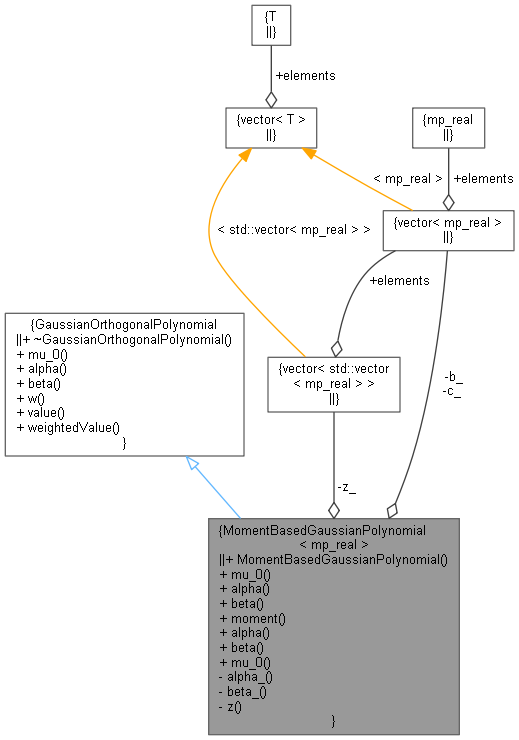
Inheritance diagram for MomentBasedGaussianPolynomial< mp_real >: Collaboration diagram for MomentBasedGaussianPolynomial< mp_real >:
Collaboration diagram for MomentBasedGaussianPolynomial< mp_real >:Public Member Functions | |
| MomentBasedGaussianPolynomial () | |
| Real | mu_0 () const override |
| Real | alpha (Size i) const override |
| Real | beta (Size i) const override |
| virtual mp_real | moment (Size i) const =0 |
| Real | alpha (Size u) const |
| Real | beta (Size u) const |
| Real | mu_0 () const |
 Public Member Functions inherited from GaussianOrthogonalPolynomial Public Member Functions inherited from GaussianOrthogonalPolynomial | |
| virtual | ~GaussianOrthogonalPolynomial ()=default |
| virtual Real | mu_0 () const =0 |
| virtual Real | alpha (Size i) const =0 |
| virtual Real | beta (Size i) const =0 |
| virtual Real | w (Real x) const =0 |
| Real | value (Size i, Real x) const |
| Real | weightedValue (Size i, Real x) const |
Private Member Functions | |
| mp_real | alpha_ (Size i) const |
| mp_real | beta_ (Size i) const |
| mp_real | z (Integer k, Integer i) const |
Private Attributes | |
| std::vector< mp_real > | b_ |
| std::vector< mp_real > | c_ |
| std::vector< std::vector< mp_real > > | z_ |
Detailed Description
class QuantLib::MomentBasedGaussianPolynomial< mp_real >
References: Gauss quadratures and orthogonal polynomials
G.H. Gloub and J.H. Welsch: Calculation of Gauss quadrature rule. Math. Comput. 23 (1986), 221-230, http://web.stanford.edu/class/cme335/spr11/S0025-5718-69-99647-1.pdf
M. Morandi Cecchi and M. Redivo Zaglia, Computing the coefficients of a recurrence formula for numerical integration by moments and modified moments. http://ac.els-cdn.com/0377042793901522/1-s2.0-0377042793901522-main.pdf?_tid=643d5dca-a05d-11e6-9a56-00000aab0f27&acdnat=1478023545_cf7c87cba4cc9e37a136e68a2564d411
Definition at line 48 of file momentbasedgaussianpolynomial.hpp.
Constructor & Destructor Documentation
◆ MomentBasedGaussianPolynomial()
Definition at line 70 of file momentbasedgaussianpolynomial.hpp.
Member Function Documentation
◆ mu_0() [1/2]
|
overridevirtual |
Implements GaussianOrthogonalPolynomial.
Definition at line 167 of file momentbasedgaussianpolynomial.hpp.
◆ alpha() [1/2]
Implements GaussianOrthogonalPolynomial.
Definition at line 143 of file momentbasedgaussianpolynomial.hpp.
◆ beta() [1/2]
Implements GaussianOrthogonalPolynomial.
Definition at line 153 of file momentbasedgaussianpolynomial.hpp.
◆ moment()
|
pure virtual |
◆ alpha_()
|
private |
Definition at line 103 of file momentbasedgaussianpolynomial.hpp.
◆ beta_()
|
private |
Definition at line 122 of file momentbasedgaussianpolynomial.hpp.
◆ z()
Definition at line 74 of file momentbasedgaussianpolynomial.hpp.
◆ alpha() [2/2]
Implements GaussianOrthogonalPolynomial.
Definition at line 138 of file momentbasedgaussianpolynomial.hpp.
◆ beta() [2/2]
Implements GaussianOrthogonalPolynomial.
Definition at line 148 of file momentbasedgaussianpolynomial.hpp.
◆ mu_0() [2/2]
|
virtual |
Implements GaussianOrthogonalPolynomial.
Definition at line 159 of file momentbasedgaussianpolynomial.hpp.
 Here is the call graph for this function:
Here is the call graph for this function:Member Data Documentation
◆ b_
|
mutableprivate |
Definition at line 65 of file momentbasedgaussianpolynomial.hpp.
◆ c_
|
private |
Definition at line 65 of file momentbasedgaussianpolynomial.hpp.
◆ z_
|
mutableprivate |
Definition at line 66 of file momentbasedgaussianpolynomial.hpp.