Base class for 1-D solvers. More...
#include <solver1d.hpp>
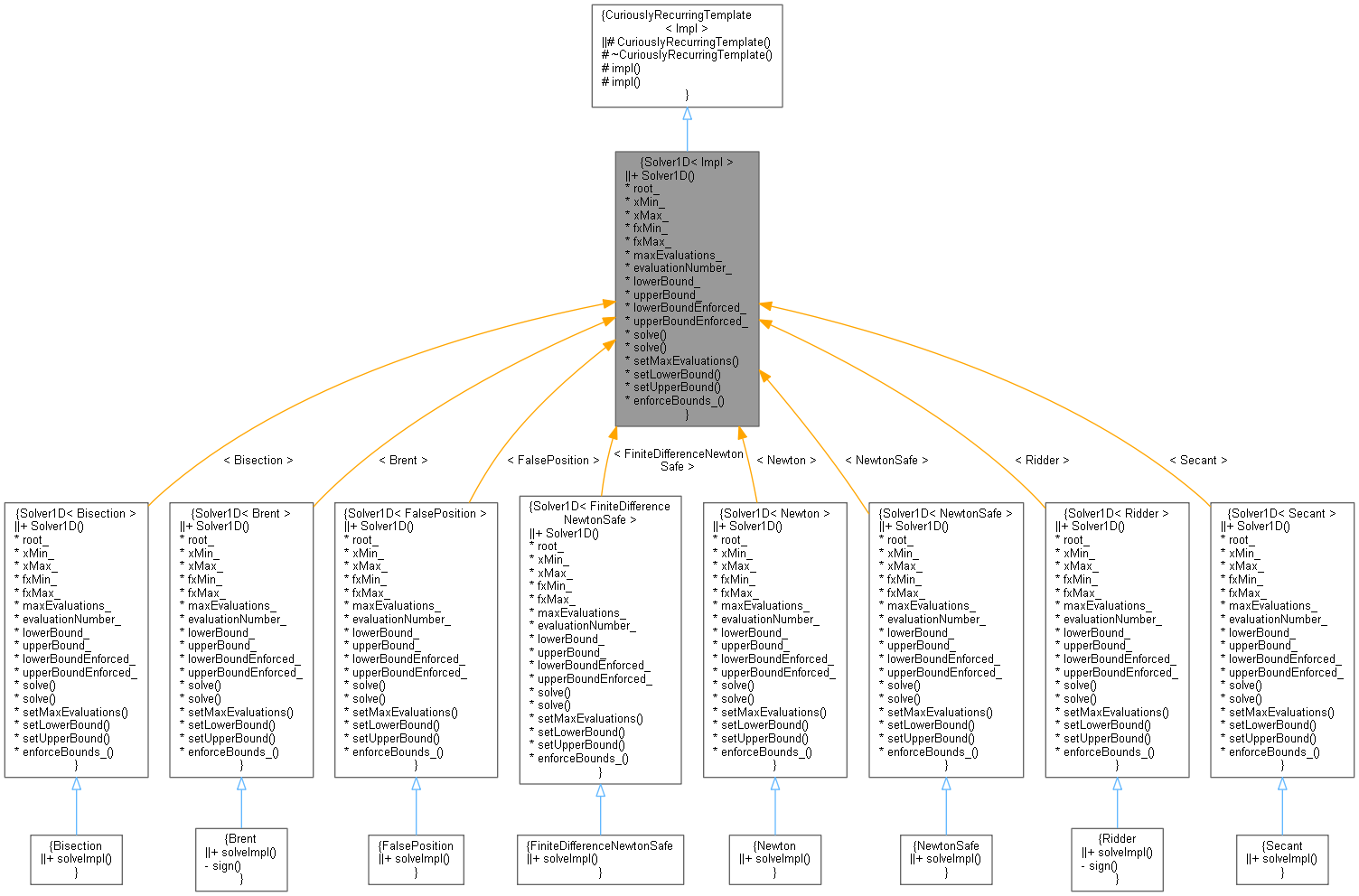
 Inheritance diagram for Solver1D< Impl >:
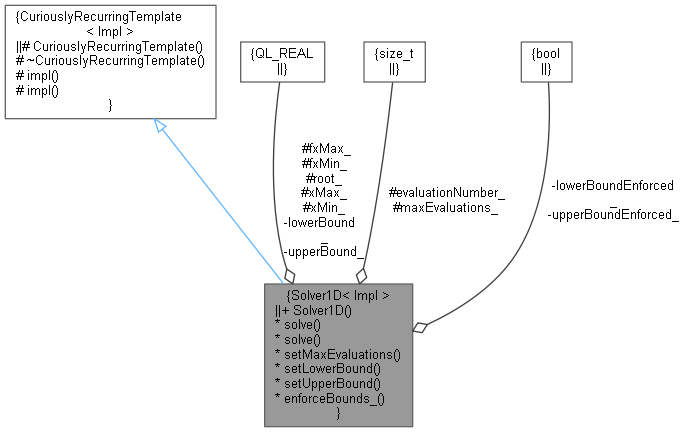
Inheritance diagram for Solver1D< Impl >: Collaboration diagram for Solver1D< Impl >:
Collaboration diagram for Solver1D< Impl >:Public Member Functions | |
| Solver1D ()=default | |
Modifiers | |
| Real | root_ |
| Real | xMin_ |
| Real | xMax_ |
| Real | fxMin_ |
| Real | fxMax_ |
| Size | maxEvaluations_ = 100 |
| Size | evaluationNumber_ |
| Real | lowerBound_ {} |
| Real | upperBound_ {} |
| bool | lowerBoundEnforced_ = false |
| bool | upperBoundEnforced_ = false |
| template<class F > | |
| Real | solve (const F &f, Real accuracy, Real guess, Real step) const |
| template<class F > | |
| Real | solve (const F &f, Real accuracy, Real guess, Real xMin, Real xMax) const |
| void | setMaxEvaluations (Size evaluations) |
| void | setLowerBound (Real lowerBound) |
| sets the lower bound for the function domain More... | |
| void | setUpperBound (Real upperBound) |
| sets the upper bound for the function domain More... | |
| Real | enforceBounds_ (Real x) const |
Additional Inherited Members | |
 Protected Member Functions inherited from CuriouslyRecurringTemplate< Impl > Protected Member Functions inherited from CuriouslyRecurringTemplate< Impl > | |
| CuriouslyRecurringTemplate ()=default | |
| ~CuriouslyRecurringTemplate ()=default | |
| Impl & | impl () |
| const Impl & | impl () const |
Detailed Description
class QuantLib::Solver1D< Impl >
Base class for 1-D solvers.
The implementation of this class uses the so-called "Barton-Nackman trick", also known as "the curiously recurring template pattern". Concrete solvers will be declared as:
Before calling solveImpl, the base class will set its protected data members so that:
xMin_andxMax_form a valid bracket;fxMin_andfxMax_contain the values of the function inxMin_andxMax_;root_is a valid initial guess. The implementation ofsolveImplcan safely assume all of the above.
Definition at line 67 of file solver1d.hpp.
Constructor & Destructor Documentation
◆ Solver1D()
|
default |
Member Function Documentation
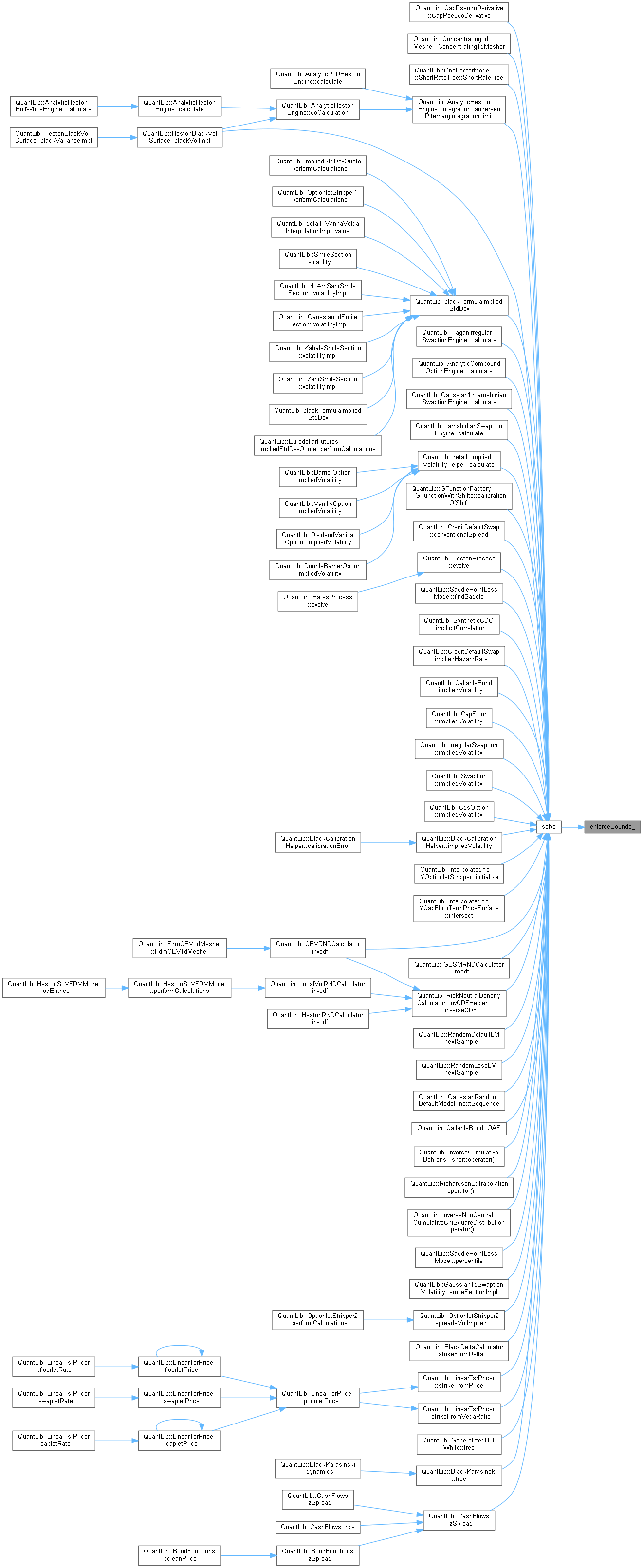
◆ solve() [1/2]
This method returns the zero of the function \( f \), determined with the given accuracy \( \epsilon \); depending on the particular solver, this might mean that the returned \( x \) is such that \( |f(x)| < \epsilon \), or that \( |x-\xi| < \epsilon \) where \( \xi \) is the real zero.
This method contains a bracketing routine to which an initial guess must be supplied as well as a step used to scan the range of the possible bracketing values.
Definition at line 84 of file solver1d.hpp.
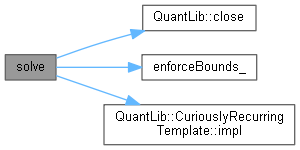
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ solve() [2/2]
This method returns the zero of the function \( f \), determined with the given accuracy \( \epsilon \); depending on the particular solver, this might mean that the returned \( x \) is such that \( |f(x)| < \epsilon \), or that \( |x-\xi| < \epsilon \) where \( \xi \) is the real zero.
An initial guess must be supplied, as well as two values \( x_\mathrm{min} \) and \( x_\mathrm{max} \) which must bracket the zero (i.e., either \( f(x_\mathrm{min}) \leq 0 \leq f(x_\mathrm{max}) \), or \( f(x_\mathrm{max}) \leq 0 \leq f(x_\mathrm{min}) \) must be true).
Definition at line 163 of file solver1d.hpp.
 Here is the call graph for this function:
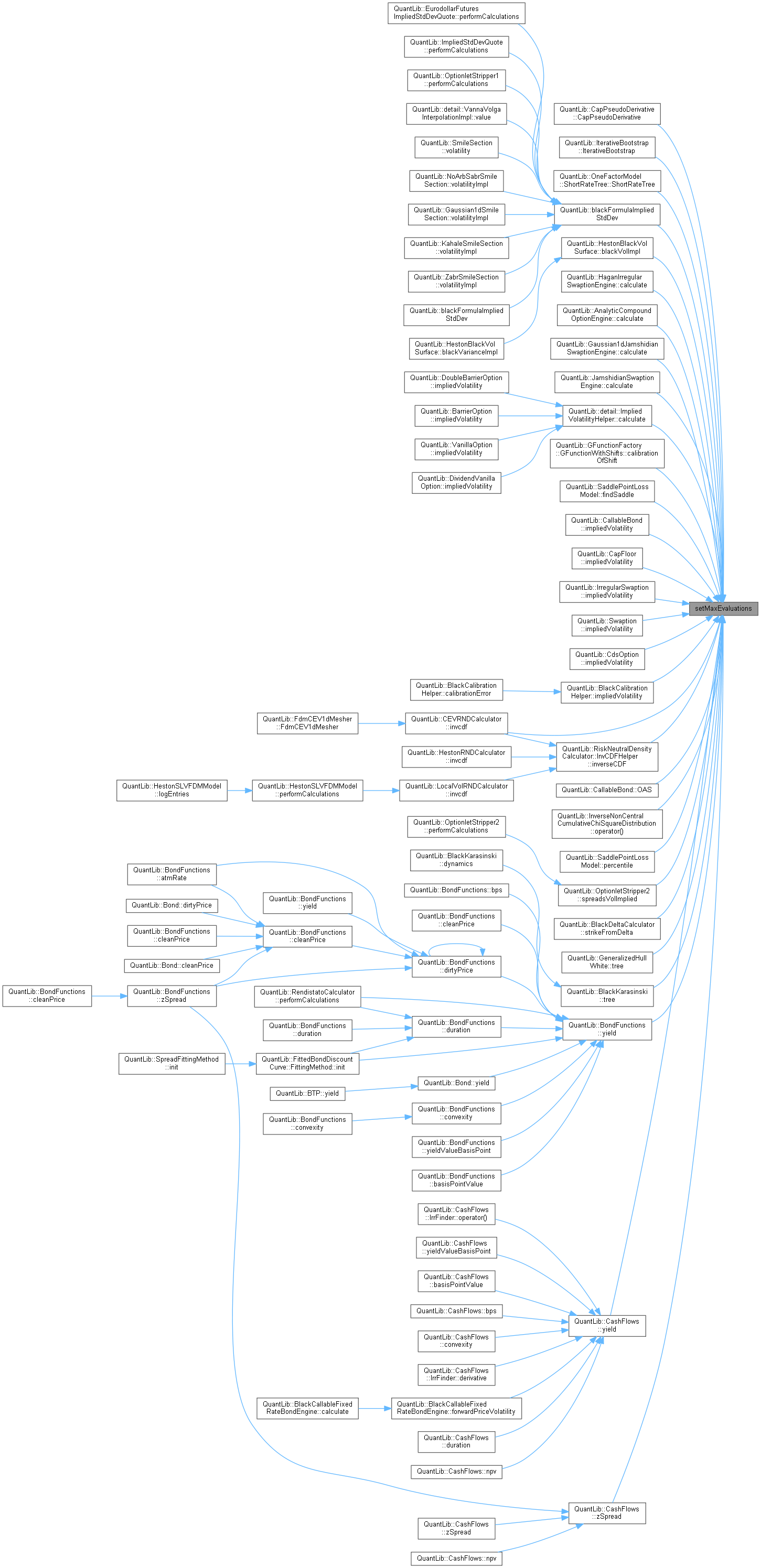
Here is the call graph for this function:◆ setMaxEvaluations()
| void setMaxEvaluations | ( | Size | evaluations | ) |
This method sets the maximum number of function evaluations for the bracketing routine. An error is thrown if a bracket is not found after this number of evaluations.
Definition at line 238 of file solver1d.hpp.
 Here is the caller graph for this function:
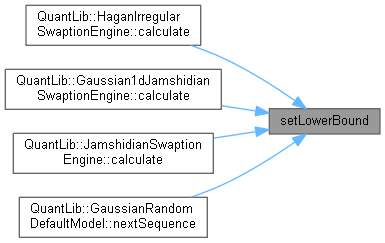
Here is the caller graph for this function:◆ setLowerBound()
| void setLowerBound | ( | Real | lowerBound | ) |
sets the lower bound for the function domain
Definition at line 243 of file solver1d.hpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ setUpperBound()
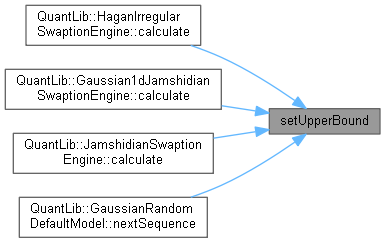
| void setUpperBound | ( | Real | upperBound | ) |
sets the upper bound for the function domain
Definition at line 249 of file solver1d.hpp.
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ enforceBounds_()
Member Data Documentation
◆ root_
|
mutableprotected |
Definition at line 225 of file solver1d.hpp.
◆ xMin_
|
protected |
Definition at line 225 of file solver1d.hpp.
◆ xMax_
|
protected |
Definition at line 225 of file solver1d.hpp.
◆ fxMin_
|
protected |
Definition at line 225 of file solver1d.hpp.
◆ fxMax_
|
protected |
Definition at line 225 of file solver1d.hpp.
◆ maxEvaluations_
|
protected |
Definition at line 226 of file solver1d.hpp.
◆ evaluationNumber_
|
mutableprotected |
Definition at line 227 of file solver1d.hpp.
◆ lowerBound_
|
private |
Definition at line 230 of file solver1d.hpp.
◆ upperBound_
|
private |
Definition at line 230 of file solver1d.hpp.
◆ lowerBoundEnforced_
|
private |
Definition at line 231 of file solver1d.hpp.
◆ upperBoundEnforced_
|
private |
Definition at line 231 of file solver1d.hpp.