Cubic interpolation between discrete points. More...
#include <cubicinterpolation.hpp>
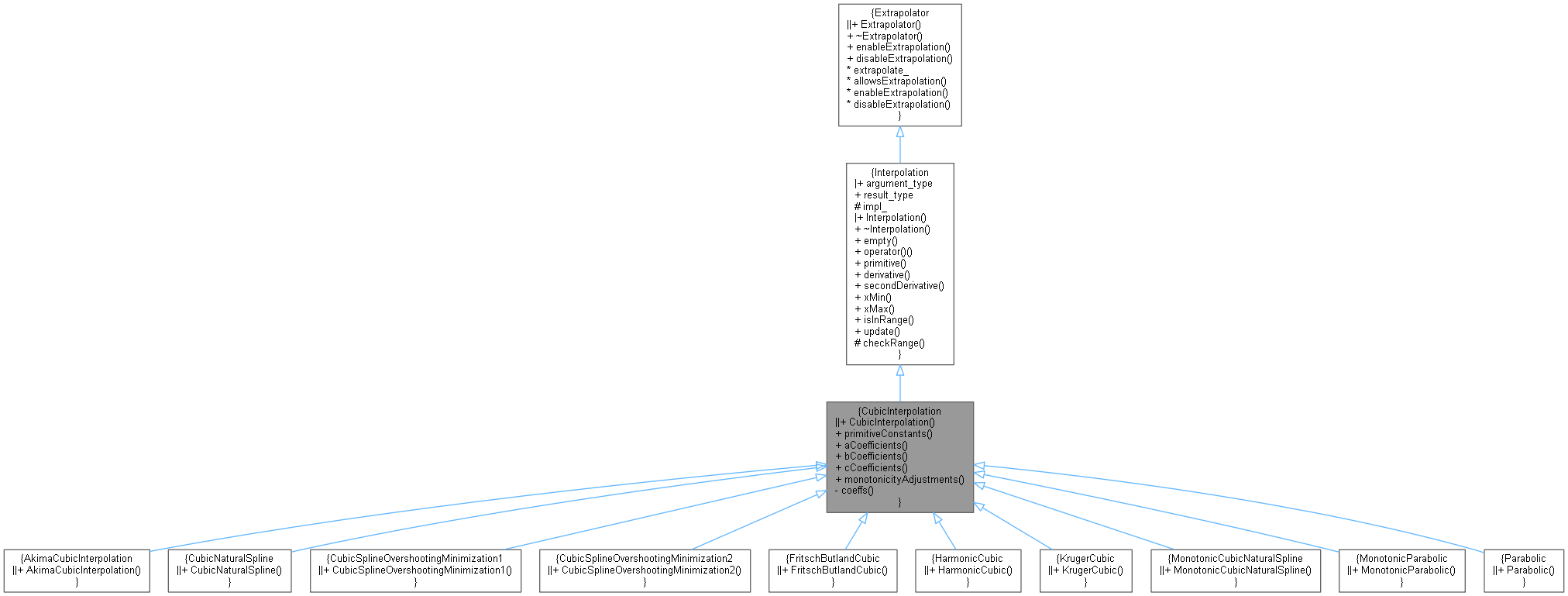
 Inheritance diagram for CubicInterpolation:
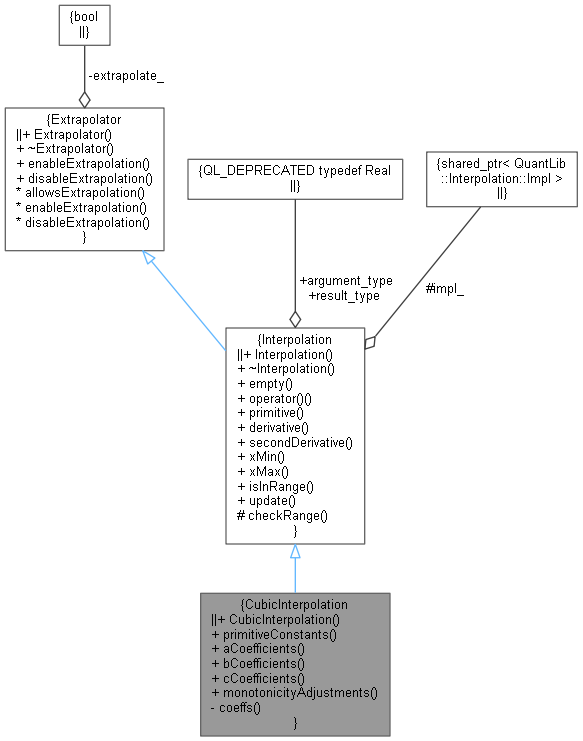
Inheritance diagram for CubicInterpolation: Collaboration diagram for CubicInterpolation:
Collaboration diagram for CubicInterpolation:Public Types | |
| enum | DerivativeApprox { Spline , SplineOM1 , SplineOM2 , FourthOrder , Parabolic , FritschButland , Akima , Kruger , Harmonic } |
| enum | BoundaryCondition { NotAKnot , FirstDerivative , SecondDerivative , Periodic , Lagrange } |
Public Member Functions | |
| template<class I1 , class I2 > | |
| CubicInterpolation (const I1 &xBegin, const I1 &xEnd, const I2 &yBegin, CubicInterpolation::DerivativeApprox da, bool monotonic, CubicInterpolation::BoundaryCondition leftCond, Real leftConditionValue, CubicInterpolation::BoundaryCondition rightCond, Real rightConditionValue) | |
| const std::vector< Real > & | primitiveConstants () const |
| const std::vector< Real > & | aCoefficients () const |
| const std::vector< Real > & | bCoefficients () const |
| const std::vector< Real > & | cCoefficients () const |
| const std::vector< bool > & | monotonicityAdjustments () const |
 Public Member Functions inherited from Interpolation Public Member Functions inherited from Interpolation | |
| Interpolation ()=default | |
| ~Interpolation () override=default | |
| bool | empty () const |
| Real | operator() (Real x, bool allowExtrapolation=false) const |
| Real | primitive (Real x, bool allowExtrapolation=false) const |
| Real | derivative (Real x, bool allowExtrapolation=false) const |
| Real | secondDerivative (Real x, bool allowExtrapolation=false) const |
| Real | xMin () const |
| Real | xMax () const |
| bool | isInRange (Real x) const |
| void | update () |
 Public Member Functions inherited from Extrapolator Public Member Functions inherited from Extrapolator | |
| Extrapolator ()=default | |
| virtual | ~Extrapolator ()=default |
| void | enableExtrapolation (bool b=true) |
| enable extrapolation in subsequent calls More... | |
| void | disableExtrapolation (bool b=true) |
| disable extrapolation in subsequent calls More... | |
| bool | allowsExtrapolation () const |
| tells whether extrapolation is enabled More... | |
Private Member Functions | |
| const detail::CoefficientHolder & | coeffs () const |
Additional Inherited Members | |
 Protected Member Functions inherited from Interpolation Protected Member Functions inherited from Interpolation | |
| void | checkRange (Real x, bool extrapolate) const |
 Protected Attributes inherited from Interpolation Protected Attributes inherited from Interpolation | |
| ext::shared_ptr< Impl > | impl_ |
Detailed Description
Cubic interpolation between discrete points.
Cubic interpolation is fully defined when the ${f_i}$ function values at points ${x_i}$ are supplemented with ${f^'_i}$ function derivative values.
Different type of first derivative approximations are implemented, both local and non-local. Local schemes (Fourth-order, Parabolic, Modified Parabolic, Fritsch-Butland, Akima, Kruger) use only $f$ values near $x_i$ to calculate each $f^'_i$. Non-local schemes (Spline with different boundary conditions) use all ${f_i}$ values and obtain ${f^'_i}$ by solving a linear system of equations. Local schemes produce $C^1$ interpolants, while the spline schemes generate $C^2$ interpolants.
Hyman's monotonicity constraint filter is also implemented: it can be applied to all schemes to ensure that in the regions of local monotoniticity of the input (three successive increasing or decreasing values) the interpolating cubic remains monotonic. If the interpolating cubic is already monotonic, the Hyman filter leaves it unchanged preserving all its original features.
In the case of $C^2$ interpolants the Hyman filter ensures local monotonicity at the expense of the second derivative of the interpolant which will no longer be continuous in the points where the filter has been applied.
While some non-linear schemes (Modified Parabolic, Fritsch-Butland, Kruger) are guaranteed to be locally monotonic in their original approximation, all other schemes must be filtered according to the Hyman criteria at the expense of their linearity.
See R. L. Dougherty, A. Edelman, and J. M. Hyman, "Nonnegativity-, Monotonicity-, or Convexity-Preserving CubicSpline and Quintic Hermite Interpolation" Mathematics Of Computation, v. 52, n. 186, April 1989, pp. 471-494.
- Tests:
- to be adapted from old ones.
- Warning:
- See the Interpolation class for information about the required lifetime of the underlying data.
Definition at line 106 of file cubicinterpolation.hpp.
Member Enumeration Documentation
◆ DerivativeApprox
| enum DerivativeApprox |
| Enumerator | |
|---|---|
| Spline | Spline approximation (non-local, non-monotonic, linear[?]). Different boundary conditions can be used on the left and right boundaries: see BoundaryCondition. |
| SplineOM1 | Overshooting minimization 1st derivative. |
| SplineOM2 | Overshooting minimization 2nd derivative. |
| FourthOrder | Fourth-order approximation (local, non-monotonic, linear) |
| Parabolic | Parabolic approximation (local, non-monotonic, linear) |
| FritschButland | Fritsch-Butland approximation (local, monotonic, non-linear) |
| Akima | Akima approximation (local, non-monotonic, non-linear) |
| Kruger | Kruger approximation (local, monotonic, non-linear) |
| Harmonic | Weighted harmonic mean approximation (local, monotonic, non-linear) |
Definition at line 108 of file cubicinterpolation.hpp.
◆ BoundaryCondition
| enum BoundaryCondition |
Definition at line 139 of file cubicinterpolation.hpp.
Constructor & Destructor Documentation
◆ CubicInterpolation()
| CubicInterpolation | ( | const I1 & | xBegin, |
| const I1 & | xEnd, | ||
| const I2 & | yBegin, | ||
| CubicInterpolation::DerivativeApprox | da, | ||
| bool | monotonic, | ||
| CubicInterpolation::BoundaryCondition | leftCond, | ||
| Real | leftConditionValue, | ||
| CubicInterpolation::BoundaryCondition | rightCond, | ||
| Real | rightConditionValue | ||
| ) |
- Precondition
- the \( x \) values must be sorted.
Definition at line 159 of file cubicinterpolation.hpp.
Member Function Documentation
◆ primitiveConstants()
| const std::vector< Real > & primitiveConstants | ( | ) | const |
◆ aCoefficients()
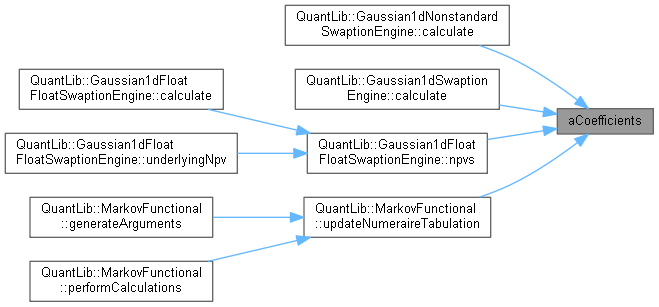
| const std::vector< Real > & aCoefficients | ( | ) | const |
Definition at line 181 of file cubicinterpolation.hpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ bCoefficients()
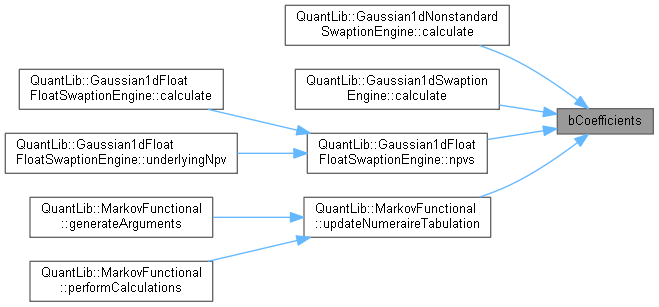
| const std::vector< Real > & bCoefficients | ( | ) | const |
Definition at line 182 of file cubicinterpolation.hpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ cCoefficients()
| const std::vector< Real > & cCoefficients | ( | ) | const |
Definition at line 183 of file cubicinterpolation.hpp.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ monotonicityAdjustments()
| const std::vector< bool > & monotonicityAdjustments | ( | ) | const |
◆ coeffs()
|
private |